勾股弦方圖

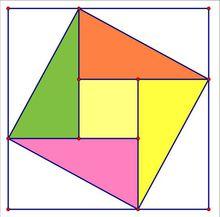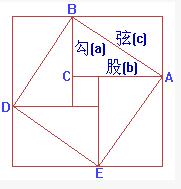
勾股弦方圖，數學術語之一，指的是是一種證明勾股定理的圖像。

勾股弦方圖是一種證明勾股定理的圖像，具體來說就是：趙爽創製了一幅“勾股弦方圖”，用數形結合的方法，給出了勾股定理的詳細證明。

在這幅“勾股弦方圖”中，以弦為邊長的正方形是由4個全等的直角三角形再加上中間的那個小正方形組成的。每個直角三角形的面積為ab/2；中間的小正方形邊長為b-a，則面積為（b-a）^2。於是便可得如下的式子：

4×（ab/2）+（b-a）^2=c^2

化簡後便可得：

勾股弦方圖

a^2+b^2=c^2