定義
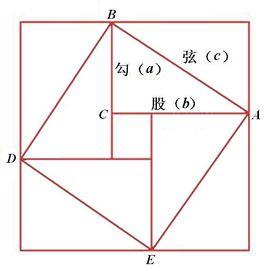
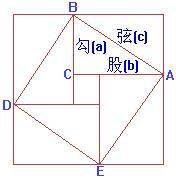 趙爽弦圖
趙爽弦圖從上面所引的這段對話中,我們可以清楚地看到,我國古代的人民早在幾千年以前就已經發現並套用勾股定理這一重要的數學原理了。稍懂平面幾何的讀者都知道,所謂勾股定理,就是指在直角三角形中,兩條直角邊的平方和等於斜邊的平方。如圖所示,我們可以看到
圖1 直角三角形
用勾(a)和股(b)分別表示直角三角形得到兩條直角邊,用弦(c)來表示斜邊,則可得:
勾的平方+股的平方=弦的平方
亦即:
a + b = c
勾股定理在西方被稱為畢達哥拉斯定理,相傳是古希臘數學家兼哲學家畢達哥拉斯於公元前550年首先發現的。其實,我國古代得到人民對這一數學定理的發現和套用,遠比畢達哥拉斯早得多。如果說大禹治水因年代久遠而無法確切考證的話,那么周公與商高的對話則可以確定在公元前1100年左右的西周時期,比畢達哥拉斯要早了五百多年。其中所說的勾3股4弦5,正是勾股定理的一個套用特例(3^2+4^2=5^2)。所以現在數學界把它稱為勾股定理,應該是非常恰當的。
在稍後一點的《九章算術》一書中,勾股定理得到了更加規範的一般性表達。書中的《勾股章》說;“把勾和股分別自乘,然後把它們的積加起來,再進行開方,便可以得到弦。”把這段話列成算式,即為:
弦的平方=勾的平方+股的平方
亦即:
c = a +b
中國古代的數學家們不僅很早就發現並套用勾股定理,而且很早就嘗試對勾股定理作理論的證明。最早對勾股定理進行證明的,是三國時期吳國的數學家趙爽。趙爽創製了一幅“勾股圓方圖”,用形數結合得到方法,給出了勾股定理的詳細證明。在這幅“勾股圓方圖”中,以弦為邊長得到正方形ABDE是由4個相等的直角三角形再加上中間的那個小正方形組成的。每個直角三角形的面積為ab/2;中間的小正方形邊長為b-a,則面積為(b-a)2。於是便可得如下的式子:
4×(ab/2)+(b-a) = c ;
化簡後便可得:
a + b = c
亦即:
c=√(a + b )
圖2 勾股圓方圖
趙爽的這個證明可謂別具匠心,極富創新意識。他用幾何圖形的截、割、拼、補來證明代數式之間的恆等關係,既具嚴密性,又具直觀性,為中國古代以形證數、形數統一、代數和幾何緊密結合、互不可分的獨特風格樹立了一個典範。以後的數學家大多繼承了這一風格並且代有發展。例如稍後一點的劉徽在證明勾股定理時也是用的以形證數的方法,只是具體圖形的分合移補略有不同而已。
影響
中國古代數學家們對於勾股定理的發現和證明,在世界數學史上具有獨特的貢獻和地位。尤其是其中體現出來的“形數統一”的思想方法,更具有科學創新的重大意義。事實上,“形數統一”的思想方法正是數學發展的一個極其重要的條件。正如當代中國數學家吳文俊所說:“在中國的傳統數學中,數量關係與空間形式往往是形影不離地並肩發展著的......”十七世紀笛卡兒解析幾何的發明,正是中國這種傳統思想與方法在幾百年停頓後的重現與繼續。”