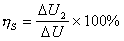動力學分析法
因為隨著化學反應的進行,反應物濃度不斷下降,反應速率逐漸降低,所以每一瞬間的反應速率都不一樣。通常採用微分的方法來表示瞬間反應速率。對下述反應:A+R→P (1)
反應速率可用單位時間內反應物濃度的降低或生成物濃度的升高來表示,即用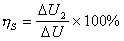 之一來表示,其中【A】t、【R】t、【P】t、是某一時刻 t時反應物A和R以及生成物P的濃度。對於式(1),可用下述動力學方程式(即速率方程式)來表示瞬間反應速率:
之一來表示,其中【A】t、【R】t、【P】t、是某一時刻 t時反應物A和R以及生成物P的濃度。對於式(1),可用下述動力學方程式(即速率方程式)來表示瞬間反應速率: 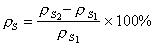 (2)
(2)
催化劑(見催化)使反應速率加快,但在一個反應體系中其濃度是恆定的,可併入動力學方程式的常數項中。溫度對反應速率的影響很大,因而常常要求在恆溫條件下進行反應。許多慢反應被痕量催化活性物質大大加速,且催化反應的速率與催化活性物質的濃度在一定範圍內呈線性關係,可用於催化活性物質濃度的測定,其靈敏度往往比平衡法高出幾個數量級。
動力學分析法的基本類型 非催化動力學分析法 用於動力學分析法的反應類型一般是二級不可逆反應,如式(1)所示。假定A是被測物,R是試劑,則反應速率如式(2)所示。最方便的測量方法是測定生成物 P或試劑R的濃度隨時間而變化的數值,測量濃度的方法可用紫外-可見分光光度法等。如果測定濃度的方法很靈敏,時間周期選擇在反應只完成2%~3%時,則生成物的【P】t很小,即式(2)中的【P】t可以忽略不計,此時式(1)成了假零級反應,式(2)變成:
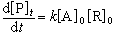 (3)
(3)
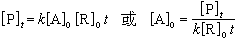 (4)
(4)
當套用固定時間法時,t恆定,試劑濃度【R】0也保持恆定,k是常數,從式(4)可見,實驗測得的【P】t值與【A】0成簡單的直線關係。如果用變動時間法,則需測量反應生成固定量的產物所必需的時間t,即【P】t和【R】0 保持恆定。從式(4)可見,1/t與【A】0也成簡單的直線關係。
對化學性質相似的混合物,例如具有同樣官能團的兩種有機物,可用示差動力學分析法,不經分離而測定各自的濃度。在式(5)和(6)所示的相互競爭的二級不可逆反應中:
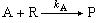 (5)
(5)
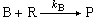 (6)
(6)
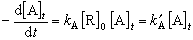 (7)
(7)
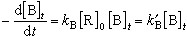 (8)
(8)
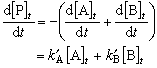 (9)
(9)
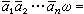 (10)
(10)

催化動力學分析法 許多慢化學反應的反應速率可被催化劑大大加速,且在一定低濃度範圍內正比於催化劑的濃度,可用來測定這些催化劑。例如對下列均相催化反應:
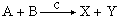 (12)
(12)
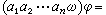 (13)
(13)
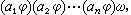 (14)
(14)
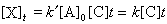 (15)
(15)
在活化劑的作用下,催化反應速率常能增大幾倍甚至幾十倍,使測定的靈敏度進一步提高。但活化劑本身並無催化作用,當對某一催化反應使用固定量的催化劑時,則在一定低濃度活化劑的範圍內,反應速率的增大與活化劑的濃度呈線性關係,可用於活化劑的測定。
阻抑劑能使某種催化劑失去催化活性,通常是由於與催化劑形成了非催化活性絡合物(見配位化合物)。當阻抑劑在一定低濃度範圍內時,則催化反應速率的降低與阻抑劑濃度呈線性關係,可用於阻抑劑的測定。此外,阻抑劑的研究和套用,也大大提高了催化動力學分析法的選擇性和套用價值。
酶催化動力學分析法 酶是一種生物催化劑,其特點是催化反應的專一性。酶催化反應的機理是:酶E與底物S先結合成中間絡合物ES,隨後分解出產物P,酶又再生:
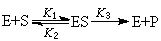 (16)
(16)
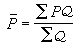 。此時的動力學方程式為:
。此時的動力學方程式為: 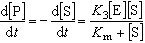 (17)
(17)
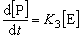 (18)
(18)
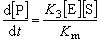 (19)
(19)
酶催化法不僅用於測定酶的活性和底物濃度,而且由於許多物質是酶的活化劑或阻抑劑,也能用於這些物質低含量時的測定。
參考書目
H.B. Mark, Jr., and G.A. Rechnitz, Kinetics in Analytical Chemistry, Interscience, New York,1968.