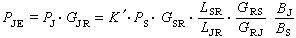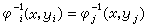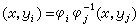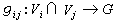N 元反應速率理論
正文
在一定的模型假定下套用統計熱力學、經典力學和量子力學等來研究元反應速率的理論,它包括簡單碰撞理論、量子力學的碰撞理論和過渡態理論。知道了一個複雜反應中各個元反應的速率,就能知道該複雜反應的速率,從而把研究化學反應速率的問題歸結為研究各元反應速率的問題。簡單碰撞理論 兩個分子必須碰到一起(稱為兩個分子發生了碰撞),然後才能起化學反應。一個分子在一秒鐘內同其他分子碰撞的次數稱為碰撞頻率。簡單碰撞理論認為,相碰分子的總動能必須大於某個值才會發生化學反應。分子碰撞而能發生化學反應的最小動能稱為臨界能Ec,Ec隨碰撞分子而異。一立方厘米體積中,兩個分子在一秒鐘內相碰撞的次數稱為碰撞速率。能夠發生化學反應的碰撞稱為有效碰撞。分子碰撞理論認為,化學反應的速率等於有效碰撞速率。
假設分子為剛球,分子A的半徑為rA,分子B的半徑為rB,每立方厘米內有nA個A分子和nB個B分子,分子A對分子B的平均相對速度為婔,則A分子同B分子的碰撞速率ZAB為:
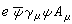
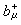
(墫AB)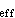 =ZABexp(-Ec/RT)
=ZABexp(-Ec/RT)
分子不是球型的,更不是剛球,所以兩個分子碰撞是否有效,還須看碰撞的方位如何。例如,氫原子同氟化氫分子的碰撞,可分為兩種方位:
H+HF─→H2+F
H+FH─→HF+H
(墫AB)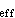 =PZABexp(-Ec/RT)
=PZABexp(-Ec/RT)
反應速率常數k等於分子濃度為1單位時的有效碰撞速率:
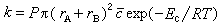
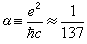 ,它與絕對溫度T 有關,而S.A.阿倫尼烏斯提出的指數定律(見活化能)的指前因子A 與溫度無關,所以Ec不等於活化能。
,它與絕對溫度T 有關,而S.A.阿倫尼烏斯提出的指數定律(見活化能)的指前因子A 與溫度無關,所以Ec不等於活化能。 量子力學的碰撞理論 分子起化學反應,是分子中的電子和原子核相互作用和運動的結果,例如以下雙分子元反應:
A+B─→C+D
分子A和分子B由彼此相距很遠,運動至相距很近,以至碰撞,從而分子A中的電子同分子B中的電子和原子核相互作用,分子相距越近,相互作用越強。這種相互作用改變電子和原子核的結合對象,使原來的分子分解,生成新分子。電子的質量比原子核的質量小很多,運動比原子核快得多。電子運動一周,原子核基本未動。因此,原子核是在電子的平均力作用下運動的,該力決定著原子核運動所受的勢能,它是原子核間距的函式,稱為勢能函式。如果勢能函式只是兩個獨立核間距的函式,則以兩個核間距為縱橫坐標對勢能函式作圖,得到一個真正的曲面,稱為勢能面。如果勢能函式是三個以上獨立核間距的函式,將勢能函式對獨立核間距作圖,則得到廣義的曲面,稱為超勢能面。
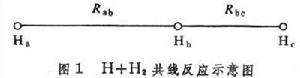
當原子與雙原子分子起反應,且三個原子在一條直線上運動時,勢能函式只是兩個獨立變數的函式,例如共線反應(圖1):
 N 元反應速率理論
N 元反應速率理論Ha+Hb-Hc─→Ha-Hb+Hc
勢能函式是兩個獨立變數核間距Rab和Rbc的函式。圖2
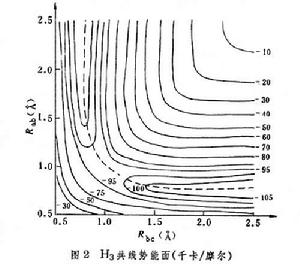 是H3的共線勢能面,當Rab趨於∞時,H3成為反應物分子,等於Ha+Hb─Hc;當Rbc趨於∞時,則H3成為產物分子,等於Ha─Hb+Hc。圖中的曲線是勢能等值線,即在此曲線上,勢能值是相等的。此圖很像一幅山區地圖,在兩邊陡峭的山間有一條小路,稱為最小能途徑,因為它是能量最低點的聯線。
是H3的共線勢能面,當Rab趨於∞時,H3成為反應物分子,等於Ha+Hb─Hc;當Rbc趨於∞時,則H3成為產物分子,等於Ha─Hb+Hc。圖中的曲線是勢能等值線,即在此曲線上,勢能值是相等的。此圖很像一幅山區地圖,在兩邊陡峭的山間有一條小路,稱為最小能途徑,因為它是能量最低點的聯線。 在反應物區和產物區的最小能途徑之間有一小的凸起區,稱為勢壘,勢壘的頂點稱為鞍點,此處的勢能圖呈馬鞍形。沿最小能途徑走向反應物區和產物區,勢能均急劇下降;沿著最小能途徑的垂直方向,則勢能急劇上升。反應開始時,基態反應分子越過勢壘所需的最小動能(E0稱為閾值能)。反應分子的總能量(以反應開始時的基態內能為標準)必須高於E0,反應才能發生。
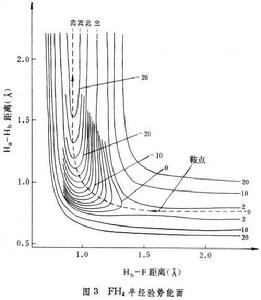
按照反應勢壘出現的位置,勢能面可分為三種:①勢壘在最小能途徑的對稱位置上。這類反應的勢能面對反應區和產物區是對稱的,即反應物和產物的性質相同。例如 H+H2─→H2+H,屬於這類反應。②勢壘在反應區,F+H2─→HF+H反應屬於此類(圖3)。這類勢壘稱為早期勢壘。③勢壘在產物區,上述反應的逆反應屬於此類,其勢壘稱為晚期勢壘。
 N 元反應速率理論
N 元反應速率理論 N 元反應速率理論
N 元反應速率理論 N 元反應速率理論
N 元反應速率理論反應坐標可用來表示反應進行的程度。圖6
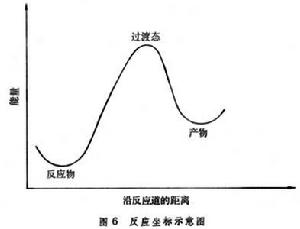 示出反應物和產物分子的勢能隨反應坐標的變化。反應坐標是化學鍵生成和分解程度的度量,在勢壘頂及其附近,反應坐標同勢能面和超勢能面的最小能途徑一致。
示出反應物和產物分子的勢能隨反應坐標的變化。反應坐標是化學鍵生成和分解程度的度量,在勢壘頂及其附近,反應坐標同勢能面和超勢能面的最小能途徑一致。 如果勢能是三個以上獨立坐標的函式,則不能用一張圖表示出勢能隨坐標的變化,須用一系列的圖才能表達。每張圖都是選定兩個獨立坐標而固定其他坐標畫出的勢能等值圖。圖7
 是固定夾角的勢能面圖。另一種是固定雙原子分子的鍵長,對夾角和一個核間距畫出的勢能面圖,但這種勢能面圖不常套用。
是固定夾角的勢能面圖。另一種是固定雙原子分子的鍵長,對夾角和一個核間距畫出的勢能面圖,但這種勢能面圖不常套用。 上面的勢能面是在二維平面上用等直線標明勢能值大小而畫出的,這是最常用的勢能面圖。有時用三維坐標直接畫出勢能的大小。但因為核間距是自0→∞,所以為了便於了解,只截出核間距為某一定值的圖(圖8)。
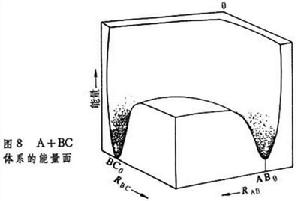 N 元反應速率理論
N 元反應速率理論A+BC─→(ABC)≠─→AB+C
式中(ABC)≠表示過渡態(凡與過渡態有關的物理量都標有“≠”)。過渡態的特徵是:①有一定的幾何構型,AB和BC的核間距均較小,但大於這兩個雙原子分子的鍵長;②能量不小於閾值能E0;③構型不穩定,壽命短於一皮秒。過渡態理論假設:①元反應均經過過渡態;②過渡態是不返回態,即過渡態只朝向產物分解,不回到反應物中去;③過渡態處於熱平衡中,在這些假設下,過渡態就像通常分子一樣,可用統計熱力學討論。
根據過渡態的假設,並假定過渡態與反應物達到化學平衡,可推導出元反應的速率公式,也稱艾林公式:
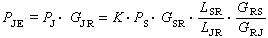
放棄過渡態同反應物達到化學平衡的假設,由量子力學(或經典力學)和統計力學可以更嚴格地推導出反應速率的表達式,它的形式與艾林公式相同。由配分函式可以寫出過渡態和反應物的平衡常數K≠: