勒貝格內測度

簡介

勒貝格內測度是勒貝格(Lebesgue,H.L.)提出他的測度定義時所用的一個輔助性概念，簡稱(L)內測度。

m*(E)=inf{G|G包含E且G為開集} 此為外測度 　m*(E)=sup(F| F包含於E且F為閉集} 此乃內測度

勒貝格最初引進勒貝格測度時，對有界集E定義，當m*(E)=m(E)時E可測，m*(E)與m(E)的公共值為E的測度。

公式

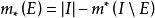勒貝格內測度

若E⊂R為有界點集，I為包含E的任一有界區間，則|I|-m*(I\E)稱為E的勒貝格內測度，記為m(E)或|E|，即，其中|I|表示區間I的體積。

勒貝格外測度

勒貝格外測度為定義點集的勒貝格測度而建立的預備性概念，簡記為(L)外測度。

外測度的概念是測度定義的基礎。

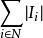勒貝格內測度

對於R 中的任一點集E，把覆蓋E的可數個開區間的體積之和的下確界稱為E的勒貝格外測度，簡稱為E的外測度，記為m*(E)或|E|，即m*(E)=inf{|{I}為覆蓋E的可數個開區間}。