簡介
勒貝格一斯蒂爾傑斯測度簡稱(L-S)測度，是直線上勒貝格測度的推廣。
設g(x)是定義在R上的單調上升的右連續函式，分三步完成相應(L-S)測度的定義：
g長度
1、左開右閉區間的g長度。對R中任一左開右閉區間1=(a,b]，稱數值(I)=g(b)-g(a)為區間I的g長度。特別地，當g(x)=x時，g長度(I)就是區間I的長度；
外測度
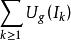勒貝格-斯蒂爾傑斯測度2、點集E的(L-S)外測度。設E為R中任一點集，把覆蓋E的可數個左開右閉區間的g長度之和的下確界稱為E的(L-S)外測度，記為*(I)，即*(E)=inf{|{I}為可數個覆蓋E的左開右閉區間}。
特別地，當g(x)=x時，*(E)即為E的(L)外測度m*(E)；當E為左開右閉區間I時，*(I)=(I)。
(L-S)測度
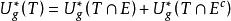勒貝格-斯蒂爾傑斯測度3、(L-S)測度。設E是R中的一點集，如果對於任意點集T，當T分解成E內部分T∩E與E外部分T∩E 時，相應的(L-S)外測度都具有可加性，即，則E稱為關於g(x)的(L-S)可測集，或稱E為*可測集或g可測集。此時E的(L-S)外測度*(E)就稱為E的由分布函式g(x)引出的(L-S)測度，並記為*(E)。
特別地，當g(x)=x時，(E)即為E的(L)測度m(E)；當E為左開右閉區間I時，它必為g可測集，且其(L-S)測度(I)與它的g長度在數值上相等。
