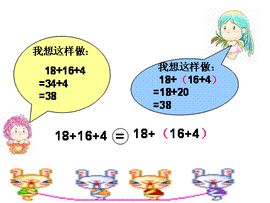
例子
字母表示:a+b+c=a+(b+c)
數字表示:18+5+15=18+(5+15)=38
證明
下面從皮亞諾公理體系出發,使用數學歸納法,給出加法結合律的一個嚴格證明。其中,S(k)表示k的後繼序數。簡單來說S(k)=k+1。
要證明(m+n)+k=m+(n+k), 對k歸納.
1. k=0, 由加法定義得(m+n)+0=m+n和m+(n+0)=m+n, 因此結合律對k=0成立.
2. 假設結論對k成立, 即(m+n)+k=m+(n+k). 下證結論對S(k)成立,
由加法定義可得: (m+n)+S(k)=S((m+n)+k);
以及m+(n+S(k))=m+S(n+k)
=S(m+(n+k))
又由歸納假設(m+n)+k=m+(n+k)
因此S((m+n)+k)=S(m+(n+k))
所以(m+n)+S(k)=m+(n+S(k))
故結論對S(k)亦成立, 由歸納公理, 結論得證.
教學
內容
九年義務教育六年制國小數學第八冊第28--29頁。
教材簡析:加法結合律這部分內容是在加法意義的基礎上進行教學的,是繼加法交換律之後的加法第二個運算定律,學好加法結合律,對於加法的簡便運算,提高計算速度和準確程度很有幫助。
由於加法結合律是在連加法運算順序發生變化結果不變基礎上,歸納概括出來的,同加法交換律相比比較抽象,因此我在設計時,注重引導學生通過實例觀察嘗試探究得出加法結合律的具體內容。這樣從具體到抽象,符合學生認知規律,不僅能夠分散教學難點,而且能突出教學重點,解決了教學關鍵,更重要的是充分發揮了學生學習的主動性和能動性。
目的
1.引導學生探索和理解加法交換律、結合律,能運用運算定律進行一些簡便計算。
2.培養學生根據具體情況,選擇算法的意識與能力,發展思維的靈活性。
3.使學生感受數學與現實生活的聯繫,能用所學知識解決簡單的實際問題。
重點
理解並掌握加法結合律。
難點
加法結合律的推導。
關鍵
通過實例引出規律。
過程
一、引入新課
李叔叔第三天的旅程已經結束了,你有什麼問題想問問李叔叔嗎?
讓學生自己回答。
李叔叔詳細的記錄了他的行程,我們來一起看看他的記錄手冊,肯定能回答大家剛才提出的問題。
二、新課學習
加法結合律
李叔叔想知道這三天一共騎了多少千米,大家能幫他解決這個問題嗎?誰來說一說用什麼法計算?怎么列式?
88+104+96
看來用這樣的一個連加的算式就能解決李叔叔的這個問題。你能用自己的方法來完成這道加法題嗎?
讓學生自己完成,然後匯報。教師巡視後,找出複合結合律的幾個學生匯報,或者投影展示。觀察這幾位同學的做法,你有什麼發現?
(88+104)+96=88+(104+96)
你還能舉出這樣的例子嗎?寫一寫。
觀察這些算式,你發現了什麼規律?
加法結合律也可以為我們的計算提供方便。想一想,你能用什麼方法來表達一下加法結合律嗎?怎么樣才能讓我們更容易記住這個規律呢?請大家動腦想一想,動手寫一寫、畫一畫。
學生匯報,鼓勵學生提出的各種不同的表示方法。引導學生了解文字、字母、符號三種表示方法。強調字母表示法是常用的表示方法,要求學生掌握。
三、鞏固練習
練一練
(1)256+99+44=(□+□)+□
(2)125+32+168=□+(□+□)
四、課堂總結
今天我們學習了加法結合律。