正文
若兩力系分別使一剛體在相同的初始運動條件下產生相同的運動則稱為等效力系。力線的平移 要使作用於剛體上A點的力F平移至另一點O（圖1）,可在O點加上大小相等、方向相反且與力F平行的兩個力F┡和F″，並使它們的大小相等。F和F″組成一力偶，稱為附加力偶。於是，作用於A點的力F可由作用於O點的力F┡和附加力偶(F，F″)來代替。換言之，要使作用於剛體上A點的力F等效地平移至O點，必須附加一個力偶，其矩等於原力對平移點O的矩。
力系的簡化 要把一個複雜的力系化為一個簡單的等效力系,可用力線的平移將力系中的諸力Fi(i=1,2,…,n）移向指定點（簡化中心）,得到一個作用在簡化中心O 的匯交力系和一個附加力偶系。此匯交力系又可合成一個合力R，它等於原力系中諸力的矢量和：
，
R為原力系的主矢。不論選何點為簡化中心,主矢的大小和方向都不變。因此，主矢與簡化中心的位置無關。簡化中引入的附加力偶系可合成一力偶，其力偶矩MO等於原力系諸力分別對簡化中心O點之矩的矢量和：
，
MO稱為原力系對簡化中心O的主矩。對於不同的簡化中心，各力的力臂也不同，因此，主矩同簡化中心的位置有關。簡化結果不外乎以下幾種情況：表明原力系和一個力偶等效,即簡化為一個力偶，其力偶矩等於力系對簡化中心的主矩。若向不同的簡化中心簡化，也將得到彼此等效的力偶。因此，簡化結果同簡化中心位置無關。這樣的力系如作用於剛體，能使剛體產生角加速度轉動。
表明原力系和一個力等效,即簡化為一個力。這樣的力系如作用於剛體，能使剛體的質心產生加速度運動。
對於空間任意力系又可分為以下四種情況：
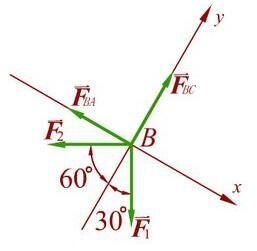
①R⊥MO 即主矢與力偶矩矢垂直,所以,主矢R與表示主矩MO的一對力（圖2中的R┡，R″）在同一平面上。改變主矩的力使其大小等於R，即R┡＝R″＝R，便可求得力偶臂。由於作用在簡化中心O的R″的方向與R相反,所以R″與R相抵消，只剩下作用於O1點的力R┡,即力系簡化為作用於O1點的一個力R┡。 ②R∥MO 原力系簡化為一個力和一個力偶，且這力垂直於力偶作用面（圖3）,稱為力螺鏇。例如鑽孔或擰螺絲釘時，作用在鑽頭或改錐上的就是力螺鏇。力螺鏇作用於剛體時，使其質心作加速度運動，同時又產生角加速度轉動。 ③R和M成任意角度 可將MO分解為平行和垂直於R的兩個分量和 。按上述兩種情形，R和可簡化為作用於O┡點的一個力R┡;而R┡和又組成一個力螺鏇(圖4)。沿R┡的作用線作直線AB。當R┡沿AB移動時,簡化結果不變(因R┡對O點之矩不變),故只要簡化中心取在AB上,力系就可簡化為力螺鏇。直線AB稱為該力系的中心軸或最小力矩軸，因為力系對不在中心軸上的任一點的主矩其與之和總是大於。
④R=，MO= 這時力系處於平衡狀態，稱為平衡力系。受平衡力系作用的物體，其質心的運動狀態不變，即保持靜止或作勻速直線運動，同時繞質心轉動的動量矩守恆。
平衡方程 力系平衡條件的數學形式。空間任意力系的平衡條件是，力系的主矢和主矩都等於零，即R=，MO=。因
，
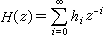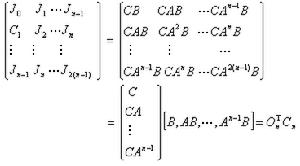，故得出空間任意力系的6個平衡方程：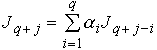 
。
平面匯交力系的平衡方程為：。
對於流體、彈性體等變形體的平衡，也可套用上述平衡方程，但還不充分（見靜力學公理）。