簡介
積分是微分的逆運算,即知道了函式的導函式,反求原函式。在套用上,積分作用不僅如此,它被大量套用於求和,通俗的說是求曲邊三角形的面積,這巧妙的求解方法是積分特殊的性質決定的。
公式種類
不定積分
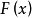 積分公式
積分公式設
是函式f(x)的一個原函式,我們把函式f(x)的所有原函式F(x)+C(C為任意常數)叫做函式f(x)的不定積分,記作,即∫f(x)dx=F(x)+C.其中∫叫做積分號,f(x)叫做被積函式,x叫做積分變數,f(x)dx叫做被積式,C叫做積分常數,求已知函式不定積分的過程叫做對這個函式進行積分。
註:∫f(x)dx+c1=∫f(x)dx+c2, 不能推出c1=c2
定積分
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。
直觀地說,對於一個給定的實函式f(x),在區間[a,b]上的定積分記為:
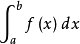 積分公式
積分公式若f(x)在[a,b]上恆為正,可以將定積分理解為在Oxy坐標平面上,曲由線(x,f(x))、直線x=a、x=b以及x軸圍成的面積值(一種確定的實數值)。
積分的種類還有如下幾類:
黎曼積分
達布積分
勒貝格積分
黎曼-斯蒂爾吉斯積分
數值積分
公式匯總
不定積分
不定積分的積分公式主要有如下幾類:含ax+b的積分、含√(a+bx)的積分、含有x^2±α^2的積分、含有ax^2+b(a>0)的積分、含有√(a²+x^2) (a>0)的積分、含有√(a^2-x^2) (a>0)的積分、含有√(|a|x^2+bx+c) (a≠0)的積分、含有三角函式的積分、含有反三角函式的積分、含有指數函式的積分、含有對數函式的積分、含有雙曲函式的積分。
含a+bx的積分
含有a+bx的積分公式主要有以下幾類:
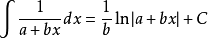 積分公式
積分公式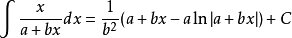 積分公式
積分公式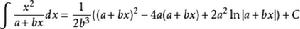 積分公式
積分公式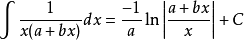 積分公式
積分公式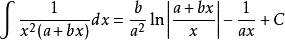 積分公式
積分公式含√(a+bx)的積分
含有√(a+bx)的積分公式只要包含有以下幾類:
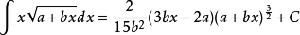 積分公式
積分公式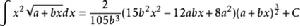 積分公式
積分公式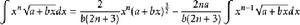 積分公式
積分公式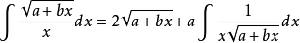 積分公式
積分公式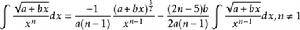 積分公式
積分公式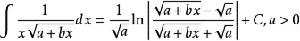 積分公式
積分公式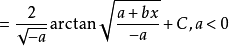 積分公式
積分公式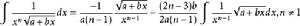 積分公式
積分公式含有x^2±α^2的積分
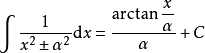 積分公式
積分公式含有ax^2+b(a>0)的積分
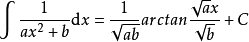 積分公式
積分公式含有√(a^2+x^2) (a>0)的積分
被積函式中含有√(a^2+x^2) (a>0)的積分有
:
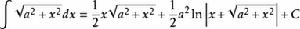 積分公式
積分公式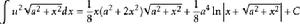 積分公式
積分公式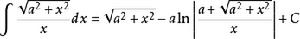 積分公式
積分公式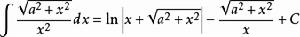 積分公式
積分公式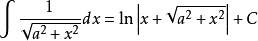 積分公式
積分公式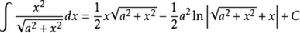 積分公式
積分公式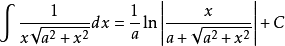 積分公式
積分公式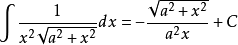 積分公式
積分公式含有√(a^2-x^2) (a>0)的積分
被積函式中含有√(a^2-x^2) (a>0)的積分有:
對於a>x有:
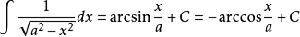 積分公式
積分公式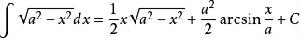 積分公式
積分公式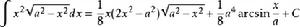 積分公式
積分公式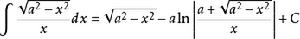 積分公式
積分公式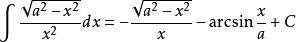 積分公式
積分公式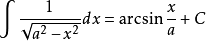 積分公式
積分公式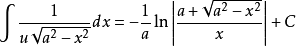 積分公式
積分公式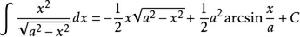 積分公式
積分公式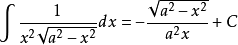 積分公式
積分公式含有√(|a|x^2+bx+c) (a≠0)的積分
被積函式中含有√(|a|x^2+bx+c) (a≠0)的積分有
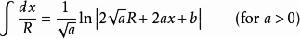 積分公式
積分公式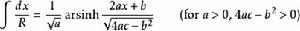 積分公式
積分公式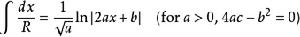 積分公式
積分公式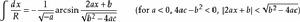 積分公式
積分公式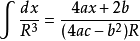 積分公式
積分公式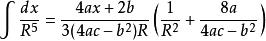 積分公式
積分公式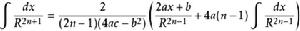 積分公式
積分公式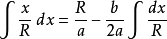 積分公式
積分公式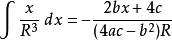 積分公式
積分公式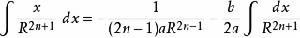 積分公式
積分公式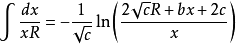 積分公式
積分公式 積分公式
積分公式含有三角函式的積分
被積函式中含有三角函式的積分公式有:
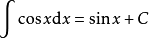 積分公式
積分公式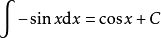 積分公式
積分公式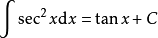 積分公式
積分公式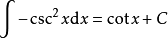 積分公式
積分公式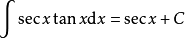 積分公式
積分公式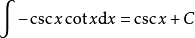 積分公式
積分公式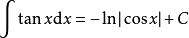 積分公式
積分公式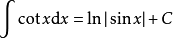 積分公式
積分公式 積分公式
積分公式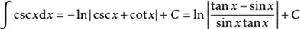 積分公式
積分公式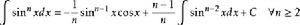 積分公式
積分公式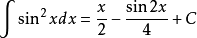 積分公式
積分公式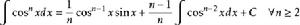 積分公式
積分公式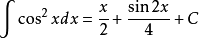 積分公式
積分公式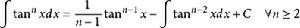 積分公式
積分公式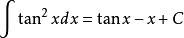 積分公式
積分公式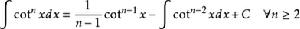 積分公式
積分公式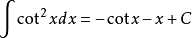 積分公式
積分公式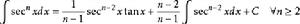 積分公式
積分公式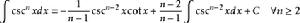 積分公式
積分公式含有反三角函式的積分
被積函式當中含有反三角函式的積分公式有
:
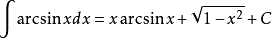 積分公式
積分公式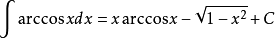 積分公式
積分公式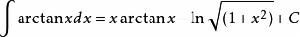 積分公式
積分公式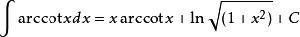 積分公式
積分公式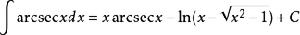 積分公式
積分公式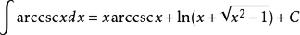 積分公式
積分公式含有指數函式的積分
被積函式當中包含有指數函式的積分公式
:
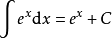 積分公式
積分公式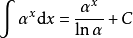 積分公式
積分公式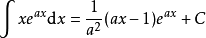 積分公式
積分公式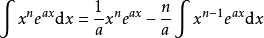 積分公式
積分公式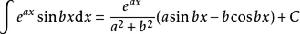 積分公式
積分公式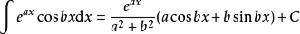 積分公式
積分公式含有對數函式的積分
被積函式當中包含有對數函式的積分公式
:
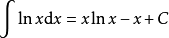 積分公式
積分公式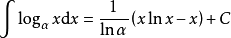 積分公式
積分公式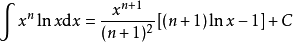 積分公式
積分公式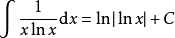 積分公式
積分公式含有雙曲函式的積分
被積函式當中包含有雙曲函式的積分公式有
:
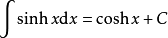 積分公式
積分公式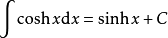 積分公式
積分公式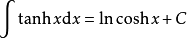 積分公式
積分公式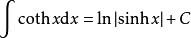 積分公式
積分公式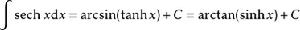 積分公式
積分公式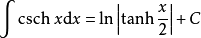 積分公式
積分公式定積分
定積分公式有以下幾種
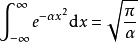 積分公式
積分公式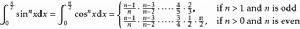 積分公式
積分公式積分性質
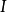 積分公式
積分公式通常意義上的積分都滿足一些基本的性質。以下積分區域
的在黎曼積分意義上表示一個區間,在勒貝格積分意義下表示一個可測集合。積分的性質有:線性性、保號性、極大值極小值、絕對連續性、絕對值積分等。
線性性
積分是線性的。如果一個函式f 可積,那么它乘以一個常數後仍然可積。如果函式f和g可積,那么它們的和與差也可積。
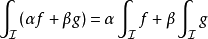 積分公式
積分公式保號性
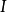 積分公式
積分公式如果一個函式f在某個區間上黎曼可積,並且在此區間上大於等於零。那么它在這個區間上的積分也大於等於零。如果f勒貝格可積並且幾乎總是大於等於零,那么它的勒貝格積分也大於等於零。作為推論,如果兩個
上的可積函式f和g相比,f(幾乎)總是小於等於g,那么f的(勒貝格)積分也小於等於g的(勒貝格)積分。
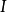 積分公式
積分公式如果黎曼可積的非負函式f在
上的積分等於0,那么除了有限個點以外,f = 0。如果勒貝格可積的非負函式f在
上的積分等於0,那么f幾乎處處為0。如果
中元素A的測度μ (A)等於0,那么任何可積函式在A上的積分等於0。
 積分公式
積分公式函式的積分表示了函式在某個區域上的整體性質,改變函式某點的取值不會改變它的積分值。對於黎曼可積的函式,改變有限個點的取值,其積分不變。對於勒貝格可積的函式,某個測度為0的集合上的函式值改變,不會影響它的積分值。如果兩個函式幾乎處處相同,那么它們的積分相同。如果對
中任意元素A,可積函式f在A上的積分總等於(大於等於)可積函式g在A上的積分,那么f幾乎處處等於(大於等於)g。
積分公式
用戶可以在Microsoft Word中創建積分公式,以Word2010軟體為例介紹操作方法:
第1步,打開Word2010文檔視窗,切換到“插入”功能區。在“符號”分組中單擊“公式”按鈕(非“公式”下拉三角按鈕)。
第2步,在Word2010文檔中創建一個空白公式框架,在“公式工具/設計”功能區中,單擊“結構”分組中的“積分”按鈕。在打開的積分結構列表中選擇合適的積分形式。
第3步,在空白公式框架中將插入積分結構,單擊積分結構占位符框並輸入具體數值或公式符號即可。

