簡介
所謂“剩餘系”,就是指對於某一個特定的正整數n,一個整數集中的數模n所得的餘數域。
如果一個剩餘系中包含了這個正整數所有可能的餘數(一般地,對於任意正整數n,有n個餘數:0,1,2,...,n-1),那么就被稱為是模n的一個完全剩餘系。
完全剩餘系
設m∈Z ,若r,r,...r為m個整數,並且兩兩模m不同餘,則r,r,...r叫作模m的一個完全剩餘系。
完全剩餘系常用性質:
1、對於n個整數,其構成模n的完系等價於其關於模n兩兩不同餘。
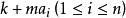 剩餘系
剩餘系2、若a(1≦i≦n)構成模n的完系,k、m∊Z,(m,n)=1,則也構成模n的完系;
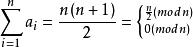 剩餘系
剩餘系3、若a(1≦i≦n)構成模n的完系,則。
簡化剩餘系
(reduced residue system)
簡化剩餘系也稱既約剩餘系或縮系,是m的完全剩餘系中與m互素的數構成的子集,如果模m的一個剩餘類里所有數都與m互素,就把它叫做與模m互素的剩餘類。在與模m互素的全體剩餘類中,從每一個類中各任取一個數作為代表組成的集合,叫做模m的一個簡化剩餘系。例如,模5的一個簡化剩餘系是1,2,3,4,模10的一個簡化剩餘系是1,3,7,9,模18的一個簡化剩餘系是1,5,7,11,13,17。
