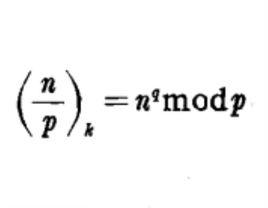k次剩餘符號

k次剩餘符號(residue sign of degree-k)是絕對最小剩餘的推廣。設k>1，p是一個奇素數，k|(p-1)，q=(p-1)/k，則稱符號(n/p)k≡n(mod p)為模p的k次剩餘符號，它表示nq對模p的絕對最小剩餘。

基本介紹

設k>1，p是一個奇素數，k|(p-1)，q=(p-1)/k，則稱符號

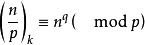k次剩餘符號

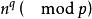k次剩餘符號

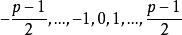k次剩餘符號

為模p的 k次剩餘符號，這裡表示n 對模p的絕對最小剩餘 。（模p絕對的最小剩餘組成的完全剩餘系是指）。

k次剩餘符號的性質

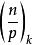k次剩餘符號

k次剩餘符號有下述性質 ：

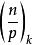k次剩餘符號

1.p|n時，=0；

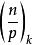k次剩餘符號

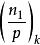k次剩餘符號

2.若n≡n(mod p)，則=；

這是因為

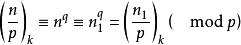k次剩餘符號

故有

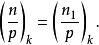k次剩餘符號

3.對任意整數n，n，有

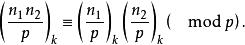k次剩餘符號

4.若indn≡a(mod k)，0≤a<k，則

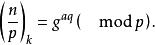k次剩餘符號

這是因為

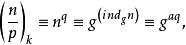k次剩餘符號

故有此結論 。

5.n是模p的k次剩餘的充分必要條件是

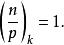k次剩餘符號

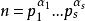k次剩餘符號

6.設n的標準分解式為，則

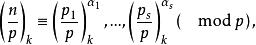k次剩餘符號

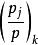k次剩餘符號

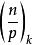k次剩餘符號

若n<p，那么只要對每一個小於p的素數p，的值都知道，之值也就可求了 。