定義
在模n的剩餘類中各取一個元素,則這n個數就構成了模n的一個完全剩餘系。
同餘式
[congruence]
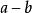 完全剩餘系
完全剩餘系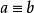 完全剩餘系
完全剩餘系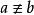 完全剩餘系
完全剩餘系命 n 為一個自然數,a,b為整數。如果 為 n 的整數倍,則稱 a,b 關於 n 同餘,用同餘式 (mod n) 記之。否則稱a,b關於 n 不同餘,記為 (mod n)。我們稱 n 為同餘式的模(modulus)。同餘式滿足:
 完全剩餘系
完全剩餘系反射性(reflection),即 (mod n);
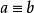 完全剩餘系
完全剩餘系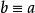 完全剩餘系
完全剩餘系對稱性(symmetry),即由 (mod n)可得 (mod n);
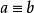 完全剩餘系
完全剩餘系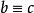 完全剩餘系
完全剩餘系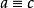 完全剩餘系
完全剩餘系傳遞性(transitivity),即由 (mod n), (mod n)可得 (mod n)。
因此,可以利用同餘關係將整數分類,凡同餘的數屬於一個類,於是異類中的數皆不同餘。共得到整數的 n 個類。在每一個類中各取一個數作為代表所成的集合稱為模 n 的一個完全剩餘系。
舉例
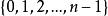 完全剩餘系
完全剩餘系 完全剩餘系
完全剩餘系 完全剩餘系
完全剩餘系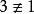 完全剩餘系
完全剩餘系取最小非負剩餘為代表,則得完全剩餘系 。剩餘類的代表相加得一數屬於另一類,這個類僅與相加兩數所在的類有關,而與代表的選取無關。於是,可以定義剩餘類間的加法,以 0 所在的類 O 為單位元,則剩餘類的全體關於加法構成一個交換群。當然在剩餘類之間可以定義乘法。但關於除法就不一定可能,例如 3·2 1·2(mod 4),2 2(mod 4),但 (mod 4)。
一個數除以4的餘數只能是0,1,2,3,{0,1,2,3}和{4,5,-2,11}是模4的完全剩餘系。可以看出0和4,1和5,2和-2,3和11模4同餘,這4組數分別屬於4個剩餘類。
性質
完全剩餘系常用性質:
性質一
對於n個整數,其構成模n的完系等價於其關於模n兩兩不同餘;
性質二
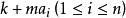 完全剩餘系
完全剩餘系若a(1≦i≦n)構成模n的完系,k、m∊Z,(m,n)=1,則也構成模n的完系;
性質三
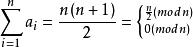 完全剩餘系
完全剩餘系若a(1≦i≦n)構成模n的完系,則。

