當代邏輯的新領域--制約邏輯
 數學邏輯
數學邏輯二千三百年前,古希臘的偉大思想家亞里士多德(Aristotelés 前384 — 前 322年)以《工具論》創立了傳統形式邏輯,為邏輯發展史樹起了第一座豐碑。從19世紀中葉到20世紀初,經過英國數學家布爾、德國數學家弗雷格、英國哲學家、數學家羅索等人接連不斷的努力,吸收萊布尼茲的成果,建立了後來作為電子計算機理論基礎的“正統數理邏輯”的觀代公理系統,這是邏輯學發展史上的第二座里程碑。
1968年,中國形式邏輯研究會理事、北京開關廠工程師林邦謹創立了一門新的邏輯學說 —— 制約邏輯,向前兩座豐碑提出了挑戰。1978年,在我國邏輯學界元老沈有鼎教授的舉薦下,經華裔美籍邏輯學家王浩教授推薦,林邦謹在美國數學會刊物《文摘》上發表論文《制約邏輯簡介》.1985年12月,林邦謹的專著《制約邏輯》在國內正式出版。制約邏輯獨樹一幟,震動了邏輯學界,引起了國內外學者的關注。
介紹
制約邏輯是傳統的形式邏輯與正統數理邏輯(現代邏輯)有機結合的產物,它運用現代邏輯提供的嚴格精密的數學方
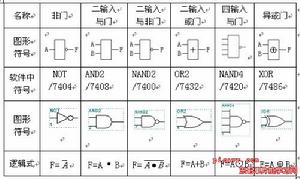 制約邏輯
制約邏輯法,去構造一個能確切地體現傳統形式邏輯的深刻正確的主導思想的非正統的邏輯制約系統。林邦謹認為,傳統形式邏輯密切結合人類普通思維和自然語言實際,把從已知進入未知的推理格式作為自己的主要研究對象,堅持貫徹不許循環論證,這是它的深刻而正確的主導思想。但它對十些極簡單的推理卻不能從理論上加;以分析,演算技術也十分簡陋、陳舊,遠不能滿足現代的需要。正統數理邏輯系統地採用了現代數學方法,論證嚴謹,演算精密,但它卻捨棄了推理格式中起決定作用的非數學的邏輯含義這一精髓,將其處理成真值函式、個體 — 真值函式關係,因而遠離了傳統形式邏輯的主導思想。林邦謹木膽地綜合融匯了上述兩種邏輯的優點而擯棄二者之缺陷,創造出自外於傳統兩家的新邏輯體系 ——制約邏輯學說,即繼承形式邏輯的正確主導思想和有效的推理格式,並採用數理邏輯所提供的數學方法來處理科學研究和社會生活中的各種邏輯問題。它是久盛不衰的傳統形式邏輯的現代發展。
制約邏輯學說指出,制約關係就是刻劃清楚後的充分條件關係。制約關係事實上構成了傳統形式邏輯中可據以進行不循環論證的推理格式的理論核心:推理式的前後件之間必定滿足普遍有效的制約關係,而在前件或後件中也必定出現制約關係。制約邏輯體系由語義學、語構學、語用學三者組成。制約邏輯語義學研究客觀世界的邏輯結構和邏輯規律,而以其中的客觀的制約關係和有關制約關係的客觀的邏輯規律為主要研究對象。制約邏輯語構學研究刻劃客觀的邏輯結構和規律的表意的人工符號的機械的排列結構和變形規則。制約邏輯語用學研究在指謂同一的原則下符號語言與自然語言的互相翻譯。總的說來,制約邏輯所研究的領域是:觀實世界對象域上的個體、集、一元或多元函式、一元:或多元關係、關係間的直值函式關係、關係間的充分條件 ( 即制約 ) 關係,和上述種種關係的客觀規律,以及它們在意識中的反映 —— 概念 ( 詞 ) 、命題和推理。其中,制約 ( 充分條件 ) 關係為研究核心。
基礎
林邦謹在深入分析人類普通的邏輯思維實際的基礎上,運用數理邏輯的演算技巧,提出了命題演算 Cm 系統和名詞演
 制約邏輯
制約邏輯算 Cn 系統。 Cm 中的“制約”命題夕 p → q 跟 p 和 q 的真假共有七種, p → q 也獲得三真四假的紀錄。這,點與萊維斯 (Lewis) 的嚴格蘊涵一致。但 Cm 跟萊維斯的模態系統是有區別的。 Cm 系統有以下主要特徵: (1) 在 Cm 中,所謂“必然”,並非某二命題的性質,而只能是兩個命題間的聯繫。 p → q 表示 p 和 q 之間有某種 " 必然 "聯繫。 (2) 除了為一般模態系統所避免的象 p → (q → p) 等著各的蘊涵怪論以外, Cm 還避免了象 T p → q 這一類最難避免因而為一般模態系統所容納的蘊涵怪論。 (3) 跟一般模態系統不同, Cn有象 [p → (q → r)] → [q → (p → r)] 這一類公式。 (4) 相當於在一般形式邏輯書中列出的傳統命題邏輯推理式的定理它都具有。 (5) 沒有象 T (pVq)—>q 這一類公式。 (6) 凡是在傳統形式邏輯中看起來好像是用了相當於被 Cm排除了的二值系統中的定理的地方, Cm 都有很好的處理方法。 在Cm系統的基礎之上建立的 Cn系統,只是擴充形式語言(引八個體變元、函式詞和謂詞),而不用量詞。這樣不僅在技巧上可避免拿有量詞的形式系統所不可避免的許多麻煩,使演算的進程原則上是命題演算,而且更接近於普通邏輯思維實際。同時, Cn系統將對解決判定問題提供明朗的前景。
意義
林邦謹在演繹推理問題上提出了兩個獨立性,具有邏輯性質“ 可獨立於前後件的真假確定不會是前真而後假”的制
 制約邏輯
制約邏輯約式定理稱為第一獨立性。具有邏輯性質“可在無需確定後件為真的情況下確定前件為真”的推理式定理稱為第二獨立性。“兩個獨立性”是為在論證中出現的推理式所必具的確保論證不循環的邏輯精髓。這是深刻的邏輯理論觀點。國內外一些專家學者認為制約邏輯在學術和科學實踐等方面有重大的意義: (1) 它可以分析、處理一系列邏輯史上迄今爭論不休、久懸末決的難題。對命題的真假對錯、主詞存在、賓詞周延和演繹推理能否推出新知,已證明的結論是否已證實,以及在數學史上引起第三次數學危機的悖論等問題,都可能給出確定的解決。 (2) 以它為邏輯基礎建立的初等數論的形式系統 N ,當 Cn 。的判定問題一經解決,就可能為最終解決哥德巴赫猜想提供新的思路。這種數論系統還可能滿足相容性和完全性 ( 與哥德爾不完全定理正好相反 ) . (3) 制約邏輯形式化公理系統,為計算機語言創造了符號語言體系。以它作為計算機科學的邏輯理論基礎,可為研究、設計新蘭代的內涵智慧型機;軟體可靠性確認、程式正確性證明等方面提供新的途徑。 (4) 以它來分析科學理論和科學創造中的邏輯機制,可使科學工作者掌握有效而實用的科學方法。
國際反映
國際邏輯學界和計算機學界對制約邏輯理論非常敏感。當林邦謹的簡短論文《制約邏輯簡介》在美國剛發表不久,聯
 制約邏輯
制約邏輯邦德國和加拿大的大學就積極組織專家研究班進行翻譯和討論,他們認為林邦謹“構造的這種邏輯體系是重要的,因為這種邏輯與計算機,科學,特別是‘判定程式'關係密切”。美國數學會秘書長利弗庫博士推薦《制約邏輯》英文摘要給下屆國。際邏輯討論會。第八屆。國際邏輯討論會第一副主席、奧地利蘭茲堡大學教授瓦因加特納博士正式邀請林邦謹參加 1987 年在莫斯科舉行的國際邏輯學術會議,並將作專題發言。在國內,林邦謹的制約邏輯現已引起學術界注意,國家科委於 1986 年在清華大學組織了高層次研討班對制約邏輯進行剖析、探討。
對《制約邏輯》的批評也是較尖銳、激烈的(郭世銘、董亦農:評《制約邏輯》中的幾個形式系統,《自然辯證法通訊》 1987, No.3)。他們認為制約邏輯的 Cm 系統與二十幾年前國外發表的相干邏輯的命題演算 R 系統形式等價,而 R 是不可判定的,那么 Cn 系統亦就是不可判定的 ( 林邦謹認為Cm 和 Cn 是可判定的)。即使假若 Cn可判定, Cn 的判定方法用到數論系統Ⅳ上去也無濟於事, 因為一階數論是不能有窮公理化的,因此要想在 Cn 基礎上構造一個滿足完全性的初等數論的形式系統N來解決哥德巴赫猜想等問題,是完全不可能的。 Cm 沒有語義學,更無語義可靠性和完全性。 Cn 無法定義“必然”、“可能”這類概念。 Cn 沒有實用價值,不可能證明任何一個有意義的必然命題和可能命題。N系統既不一致,也無足夠的表達能力,當然也不可能完全,而且沒有可判的公理集。N系統無法定義“整數”、“素數”、“減”之類的基本數論概念,無法表示象歌德巴赫猜想這類的命題。因此,N系統是一個罕見的百病纏身的系統。
那么,制約邏輯何處為真理,何處是謬誤;對它的學術性地位將怎樣做成歷史性的評價;究竟會有多大作為;是不是邏輯學上的一次革命;它能否經受得住社會實踐的考驗;相信時間終將會給予我們確切的答案。
