概念
利特爾法則(英語:Little's law),基於等候理論,由約翰·利特爾在1954年提出。利特爾法則可用於一個穩定的、非占先式的系統中。其內容為:
在一個穩定的系統(L)中,長期的平均顧客人數,等於長期的有效抵達率(λ),乘以顧客在這個系統中平均的等待時間(W);或者,我們可以用一個代數式來表達:
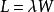 利特爾法則
利特爾法則利特爾法則可用來確定在途存貨的數量。此法則認為,系統中的平均存貨等於存貨單位離開系統的比率(亦即平均需求率)與存貨單位在系統中平均時間的乘積。
雖然此公式看起來直覺性的合理,它依然是個非常傑出的推導結果,因為此一關係式“不受到貨流程分配、服務分配、服務順序,或任何其他因素影響”。
此一理論適用於所有系統,而且它甚至更適合用於系統中的系統。舉例來說,在一間銀行里,顧客等待的隊伍就是一個子系統,而每一位櫃員也可以被視為一個等待的子系統,而利特爾法則可以套用到任何一個子系統,也可以套用到整個銀行的等待隊伍之母系統。
唯一的條件就是,這個系統必須是長期穩定的,而且不能有插隊搶先的情況發生,這樣才能排除換場狀況的可能性,例如開業或是關廠。
排隊論
排隊論(英語:queuing theory),或稱 隨機服務系統理論、 排隊理論,是數學運籌學的分支學科。它是研究服務系統中排隊現象隨機規律的學科。廣泛套用於電信,交通工程,計算機網路、生產、運輸、庫存等各項資源共享的隨機服務系統,和工廠,商店,辦公室和醫院的設計。
排隊論研究的內容有3個方面:統計推斷,根據資料建立模型;系統的性態,即和排隊有關的數量指標的機率規律性;系統的最佳化問題。其目的是正確設計和有效運行各個服務系統,使之發揮最佳效益。

