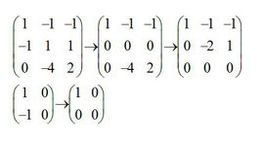初等變換
線性方程組
所謂一般線性方程組,是指形式為:
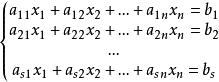 初等變換
初等變換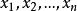 初等變換
初等變換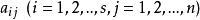 初等變換
初等變換 初等變換
初等變換的方程組,其中,代表n個未知數,s 是方程的個數,稱為方程組的係數, 稱為常數項。
初等變換
一般採用消元法來解線性方程組,而消元法實際上是反覆對方程進行變換,而所做的變換也只是以下三種基本的變換所構成:
(1)用一非零的數乘以某一方程
(2)把一個方程的倍數加到另一個方程
(3)互換兩個方程的位置
於是,將變換(1)、(2)、(3)稱為線性方程組的初等變換。
矩陣初等變換
矩陣的初等變換又分為矩陣的初等行變換和矩陣的初等列變換。矩陣的初等行變換和初等列變換統稱為初等變換。另外:分塊矩陣也可以定義初等變換。
定義:如果B可以由A經過一系列初等變換得到,則稱矩陣A與B稱為等價
初等行變換
定義:所謂數域P上矩陣的初等行變換是指下列3種變換:
1)以P中一個非零的數乘矩陣的某一行
2)把矩陣的某一行的c倍加到另一行,這裡c是P中的任意一個數
3)互換矩陣中兩行的位置
 初等變換
初等變換一般來說,一個矩陣經過初等行變換後就變成了另一個矩陣,當矩陣A經過初等行變換變成矩陣B時,一般寫作
可以證明:任意一個矩陣經過一系列初等行變換總能變成階梯型矩陣。
初等列變換
同樣地,定義初等列變換,即:
1)以P中一個非零的數乘矩陣的某一列
2)把矩陣的某一列的c倍加到另一列,這裡c是P中的任意一個數
3)互換矩陣中兩列的位置
初等矩陣
定義:由單位矩陣E經過一系列初等變換得到的矩陣稱為初等矩陣。
 初等變換
初等變換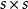 初等變換
初等變換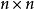 初等變換
初等變換引理:對一個矩陣A作一初等行變換,就相當於在A的左邊乘上相應的的初等矩陣;對A作一初等列變換,就相當於在A的右邊乘上相應的的初等矩陣。
行列初等變換
相關性質
性質1:行列互換,行列式不變
性質2:一數乘行列式的一行就相當於這個數乘此行列式
性質3:如果行列式中有兩行相同,那么行列式為0,所謂兩行相同,即兩行對應的元素都相等
性質4:如果行列式中,兩行成比例,那么該行列式為0
性質5:把一行的倍數加到另一行,行列式不變
性質6:對換行列式中兩行的位置,行列式反號
初等變換
以下為行列式的初等變換:
1)換行變換:交換兩行(列)。
2)倍法變換:將行列式的某一行(列)的所有元素同乘以數k。
3)消法變換:把行列式的某一行(列)的所有元素乘以一個數k並加到另一行(列)的對應元素上。
基於行列式的基本性質,對行列式作初等變換,有如下特徵:
換法變換的行列式要變號;倍法變換的行列式要變k倍;消法變換的行列式不變。求解行列式的值時可以同時使用初等行變換和初等列變換。