初等變換法
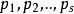矩陣求逆求元索為具體數字的矩陣的逆矩陣，常用初等變換法‘如果A可逆，則A’可通過初等變換，化為單位矩陣 I ，即存在初等矩陣使 ：
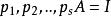矩陣求逆（1） ；
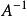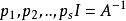矩陣求逆
矩陣求逆（2）用 右乘上式兩端，得： ；
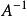矩陣求逆比較（1）、（2）兩式，可以看到當A通過初等變換化為單位處陣的同時，對單位矩陣I作同樣的初等變換，就化為A的逆矩陣 。
用矩陣表示：
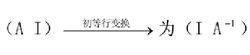矩陣求逆這就是求逆矩陣的初等行變換法，它是實際套用中比較簡單的一種方法。需要注意的是，在作初等變換時只允許作行初等變換。同樣，只用列初等變換也可以求逆矩陣。
伴隨陣法
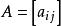矩陣求逆定理：n階矩陣 為可逆的充分必要條件是A非奇異，且：
矩陣求逆
矩陣求逆
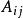矩陣求逆其中， 是|A|中元素 的代數餘子式；矩陣
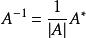矩陣求逆
矩陣求逆稱為矩陣A的伴隨矩陣，記作A*，於是有 。
用此方法求逆知陣，對於小型矩陣，特別是二階方陣求逆既方便、快陣，又有規律可循。因為二階可逆矩陣的伴隨矩陣，只需要將主對角線元素的位置互換，次對角線的元索變號即可。
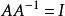矩陣求逆若可逆矩陣是二階或二階以上矩陣，在求逆矩陣的過程中，需要求9個或9個以上代數餘子式，還要計算一個三階或三階以上行列式，工作量大且中途難免出現符號及計算的差錯。對於求出的逆炬陣是否正確，一般要通過 來檢驗。一旦發現錯誤，必須對每一計算逐一排查。
定義法和恆等變形法
利用定義求逆矩陣
定義：設A、B都是n階方陣，如果存在n階方陣B使得AB=BA=E，則稱A為可逆矩陣，而稱B為A的逆矩陣。下面舉例說明這種方法的套用。
恆等變形法
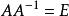矩陣求逆恆等變形法求逆矩陣的理論依據為逆矩陣的定義，此方法也常用與矩陣的理論推導上，就是通過恆等變形把要求的值化簡出來，題目中的逆矩陣可以不求，利用 ，把題目中的逆矩陣化簡掉 。
