預備知識
鄰域與有界集
設X是一個距離空間，A是X的一個子集，若存在x0∈X，及r>0，記
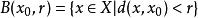列緊集
列緊集
列緊集
列緊集稱 為 的一個r鄰域，或簡稱鄰域，使得 ，則稱A為有界集。
內點與開集
設M為距離空間X的子集，如果存在x的一個鄰域整個包含於M，則稱x∈M是M的一個內點。若M的所有點都是內點，則稱M為開集。
完全有界的
設M是距離空間X中的一個子集，ε>0，N⊂M，若對任意x∈M，總存在y∈N，使得d(x,y)<ε，那么稱N是M的一個ε-網；如果N中只有有限多個點，則稱N為M的一個有限ε-網。
設A是距離空間X中的點集，如果對於任給的ε>0，A總存在有限的ε-網，則稱A是完全有界的。
自列緊集
距離空間中，閉的列緊集稱為自列緊集。
定義
表述一
列緊集(sequentially compact set)是度量空間中的一類子集。設A是度量空間X中的無窮集，如果A中的任一無窮子集必有一個收斂的點列，就稱A是X中的列緊集。如果X本身是列緊集，就稱X是列緊距離空間，簡稱為列緊空間。
表述二
設X是任一拓撲空間，又A⊂X，如果A的每個無窮子集都至少有一個聚點屬於X，則A叫做拓撲空間X的一個列緊集。如果X作為空間X的點集是列緊的，則拓撲空間X叫做一個列緊空間。例如，任意空間的所有有限點集是列緊的；空集是列緊集I有限空間為列緊空間，列緊空間的每個閉集都是列緊集；每一個緊緻空間都是列緊空間。
性質
有界集與列緊集
列緊集（1）在 中，任意有界集是列緊集。 例如，根據包查諾-魏爾史特拉斯（Bolzano-Weierstrass）定理，數值線上任何有界集必是列緊的。
列緊集（2）在 中，任意有界閉集是自列緊集。
（3）列緊集的無窮子集是列緊集。
列緊空間的子集
（1）列緊空間內任意子集都是列緊集。
（2）列緊空間內任意閉列緊集都是自列緊集。
（3）列緊空間必是完備空間。
必要條件和充要條件
（1）距離空間X中集合是列緊的必要條件是M為完全有界的。
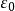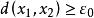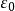列緊集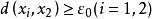
列緊集
列緊集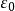 列緊集
列緊集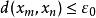 列緊集
列緊集證明：設A為距離空間X的列緊集。如果A不是全有界的，則必存在某個 ，使得A沒有有限的 網。於是對於任意抽取的x1∈A，必存在x2∈A使得 ，否則{x1}就是A的一個有限 網。同理，存在x3∈A使得 ，否則{x1,x2}就是A的一個有限 網，這樣可以一直進行下去，於是我們得到一個點列{xn}使得當m≠n時， ，{xn}顯然沒有收斂的子列，與A的列緊性相矛盾，故A為完全有界的。
（2）完備距離空間X中集合是列緊的充分必要條件是M為完全有界的。
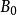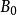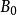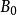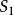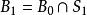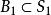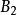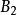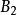列緊集 列緊集 列緊集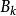 列緊集
列緊集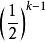 列緊集 列緊集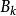 列緊集
列緊集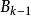
列緊集
列緊集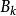
列緊集 列緊集 列緊集 列緊集 列緊集
列緊集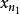 列緊集 列緊集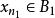 列緊集
列緊集
列緊集
列緊集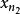
列緊集 列緊集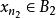
列緊集 列緊集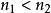 列緊集 列緊集
列緊集
列緊集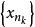 列緊集
列緊集
列緊集
列緊集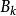 列緊集
列緊集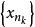
列緊集 列緊集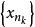 列緊集 列緊集證明：設A為完備的距離空間，A⊂X為全有界集．任取A中的一個點列，如果中只有有限個互不相同的元素，則顯然含有收斂的子列，因此，可設中有無限多個互不相同的元素，記這些元素構成的集合為。是全有界的，於是X中存在有限個以1/2為半徑的開球使得這些開球的並包含，因此它們中至少有一個開球包含了中無限多個元素，這些元素構成的集合記為，這個開球記為，即，則，且是無窮集。本身也是全有界的，將以上的論證套用於，則存在的子集，使得中含有中無限多個元素且的直徑不大於1/2。依此類推，我們可以找到一系列的集合滿足如下條件：，而且的直徑不大於。每個均含有中無限多個元素。注意到每箇中的所有元素都是中的某些項，對於k=1，可取中的某一項，使得。對於k=2，可取中的某一項使得且可設，依此類推，便得到的一個子列使得。根據的性質，是基本點列，又因為X是完備的，故在X中收斂，於是A是列緊的。
（3）設X是一個距離空間，M⊂X是緊集的充分必要條件為M是自列緊的。
Arzelá-Ascoli定理
X是列緊空間，F⊂C(X)是列緊的充要條件是F是一致有界並且等度連續的。
