簡介
強列緊是與強收斂相聯繫的列緊性。
設X是賦范線性空間,S是X的子集,如果S中任何點列都有強收斂(即按範數收斂)的子列,則稱S是強列緊的。
賦范線性空間是有限維的充分必要條件是每個有界集都是強列緊的。
強收斂
強收斂是指測度網(或列)依範數(能量)的收斂。關於點列的收斂性包括兩種:強收斂和弱收斂,並且它們之間存在著這樣的關係:強收斂必定弱收斂,但弱收斂不一定強收斂。
 強列緊
強列緊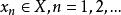 強列緊
強列緊 強列緊
強列緊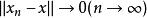 強列緊
強列緊 強列緊
強列緊 強列緊
強列緊設是賦范線性空間,,如果存在,使得,則稱點列強收斂於。
賦范線性空間
(normed linear space)
賦范線性空間是線上性空間中引進一種與代數運算相聯繫的度量,即由向量範數誘導出的度量。賦范線性空間稱為Banach空間,是指由範數導出的度量是完備的。
 強列緊
強列緊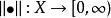 強列緊
強列緊 強列緊
強列緊定義:設是線性空間,函式稱為上定義的一個範數,如果滿足:
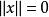 強列緊
強列緊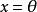 強列緊
強列緊(1)若且唯若;
 強列緊
強列緊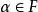 強列緊
強列緊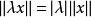 強列緊
強列緊(2)對任何及,;
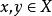 強列緊
強列緊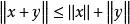 強列緊
強列緊(3)對任意,。
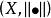 強列緊
強列緊稱二元體為賦范線性空間。
