基本介紹
收斂集列定義 對於空間X的子集列，考慮下述條件：
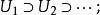收斂集列(1)
收斂集列(2) 若令，則K為非空緊集；
(3) 上述K為非空可數緊集；
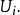收斂集列(4) K的任意鄰域含有某個
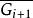收斂集列 收斂集列 收斂集列
收斂集列滿足(1)，(2)，(4)時，稱為收斂於K，滿足(1)，(3)，(4)時，稱為擬收斂於K。設是空間X的(擬)收斂集列，若集列{G}滿足∅≠G⊂U與⊂G(對於任意i)，則{G}是(擬)收斂集列，(擬)收斂集列的連續像是(擬)收斂集列 。
收斂集列的等價命題
下面是一組收斂集列的等價命題：
1.集列{A}收斂於A。
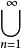收斂集列
收斂集列
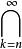收斂集列2.(A)=A=A。
3.集列{A}的任何子列收斂於A 。
相關概念及結論
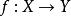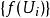收斂集列 收斂集列
收斂集列命題若為連續映射，且為X的收斂集列，則為Y的收斂集列。
這個命題收斂改為擬收斂命題也是成立的。
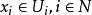收斂集列
收斂集列
收斂集列定義 空間X是點可數型(point-countable type)或擬點可數型是指對於X的任一點x，存在它的開鄰域列是收斂或擬收斂的，X是點可數型的充要條件是任意點被具有可數特徵的緊集包含。X是q空間是指若對於X的任意點x，存在它的鄰域列，使得若，則點列具有接觸點。
命題 (1) 可數型空間是點可數型的。
(2) 點可數型空間是擬點可數型的。
(3) 擬點可數型空間是q空間。
(4) 正則q空間是擬點可數型的 。
