定義
開覆蓋
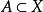緊緻集定義1 設X為非空集，{A}是X中的一族子集， ，如果
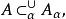緊緻集則稱集合族{A}是A的一個 覆蓋。
註：1）如果{A}中任意有限個集合之交非空，則稱{A}具有 有限交性質。
2）在定義1中，當{A}是X中的開集族時，稱其為A的 開覆蓋。
緊緻集（緊集）
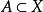緊緻集定義2 設X為拓撲空間， ，如果在任何一個覆蓋A的開集族中總可取到有限個開集覆蓋A，則稱A是X 中的 緊緻集，簡稱 緊集。
局部緊
定義3 拓撲空間X稱為 局部緊的，是指X中每一點都有閉包為緊的鄰域。
例如，按通常的拓撲，R 是非緊的，但它卻是局部緊的。
性質
性質1 Hausdorff空間X中的緊集必是閉集。
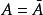緊緻集證明：設A 為Hausdorff空間X中的緊集，今證 . 若不然，必有A的聚點x，x∉A. 利用Hausdorff分離性，對任何x∈A，必有x的鄰域U和x的鄰域U'，使U∩U'=∅. 顯然，{U|x∈A}是A的一個開覆蓋。根據A 的緊性，存在它的一個有限子覆蓋，設為{U| i=1,2，...，n}. 記
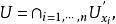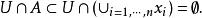緊緻集
緊緻集於是，U是x的一個領域，且 這矛盾於x是A的聚點。證畢。
註：1）若拓撲空間中任意兩個不同的點有互不相交的鄰域，則稱該拓撲空間滿足T分離公理，也稱該拓撲空間為Hausdorff空間。
2）拓撲空間的緊集未必是閉集。
性質2 緊集的閉子集是緊集。
證明：設A 是拓撲空間X中的緊集，B是其閉子集，設{F}為閉子集族，且{F∩B}具有有限交性質。注意到（F∩B）∩A=F∩B，對閉子集族{F∩B}而言，{（F∩B）∩A}具有有限交性質。由A的緊性，利用下面的定理1，得：（∩F）∩B=[∩（F∩B）]∩A≠∅，因而B是緊集。證畢。
性質3 拓撲空間中有限個緊集的並仍為緊集，兩個緊集的交未必是緊的，但閉且緊的子集的任意交是閉且緊的。
性質4 拓撲空間的緊集的閉包可以不是緊的，但T空間的緊集的閉包是緊的。
證明緊集的方法
定理1 A是拓撲空間X中的緊集的充要條件是對X中任何閉集族{F}，如果{F∩A}具有有限交性質，則（∩F）∩A=∅.
定理2 設X為距離空間，M是X的子集，則M為緊集的充要條件是M為列緊閉集。
定理3 有限維賦范線性空間中的有界閉集是緊集。
註：1）定理1-3的證明見參考文獻[2]的19-27頁。
2）由定理2可知：A是距離空間X中緊集的充要條件是A 中任何點列必有在A中收斂的子列。
常用結論及拓展
1.設X是無限維的賦范線性空間，則X中的單位球{x | ||x|| ≤1}非緊。
證明：證明見參考文獻[2]的28頁。
利用定理4的結論，不難證得：若E是無限維的Banach空間，I：E→E為恆等運算元，則I不是緊運算元。
2.記緊空間X上的連續函式全體為C（X），對f∈C（X），記
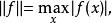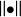緊緻集
緊緻集則C（X）按 為一個Banach空間。
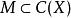緊緻集3.設X是緊距離空間， ，可利用Arzela-Ascoli定理來證明M的列緊性。
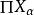緊緻集4.（Tychonov定理）設Xα是緊拓撲空間，則其乘積空間 也是緊的。
