簡介
多項式緊運算元是緊運算元概念的推廣。
設T是賦范空間 X 上的有界線性運算元,如果存在非零多項式
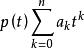 多項式緊運算元
多項式緊運算元使
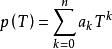 多項式緊運算元
多項式緊運算元為緊運算元,則稱 T 是多項式緊運算元,代數運算元是多項式緊運算元的重要例子。
緊運算元
緊運算元是一類重要的有界運算元,它最接近於有限維空間上的線性運算元。
設X,Y是賦范線性空間,A是X到Y的連續運算元。如果A把定義域中任何有界集映射成Y中的列緊集,則稱A是緊運算元,或全連續運算元。
有界線性運算元
有界線性運算元是泛函分析中一種重要的運算元。
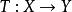 多項式緊運算元
多項式緊運算元 多項式緊運算元
多項式緊運算元 多項式緊運算元
多項式緊運算元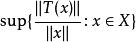 多項式緊運算元
多項式緊運算元 多項式緊運算元
多項式緊運算元 多項式緊運算元
多項式緊運算元 多項式緊運算元
多項式緊運算元 多項式緊運算元
多項式緊運算元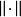 多項式緊運算元
多項式緊運算元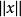 多項式緊運算元
多項式緊運算元 多項式緊運算元
多項式緊運算元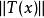 多項式緊運算元
多項式緊運算元 多項式緊運算元
多項式緊運算元設是從線性賦范空間到的線性運算元。 如果當存在且有限,則稱是有界線性運算元,也就是說將中的每個有界集映射為中的有界集。此處|表示範數,表示中定義的範數,表示中定義的範數。
