概念
緊收斂拓撲(topology of compact conver-gence)是映射空間上一類常見的拓撲。設F為集合X到一致空間(Y,V)的映射族,A為X的非空子集族。對於A∈A,V∈V,若:
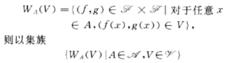 緊收斂拓撲
緊收斂拓撲為子基在F上生成的一致結構稱為在A的成員上一致收斂的一致結構。特別地,當F為拓撲空間X到一致空間(Y,V)的所有連續映射的族,並且A為X的所有緊子集的族時,上述一致結構稱為在緊集上的一致收斂的一致結構。它的拓撲稱為緊收斂拓撲。緊收斂拓撲就是緊開拓撲。
拓撲空間
拓撲空間是歐幾里得空間的一種推廣。給定任意一個集,在它的每一個點賦予一種確定的鄰域結構便構成一個拓撲空間。拓撲空間是一種抽象空間,這種抽象空間最早由法國數學家弗雷歇於1906年開始研究。1913年他考慮用鄰域定義空間,1914年德國數學家豪斯多夫給出正式定義。豪斯多夫把拓撲空間定義為一個集合,並使用了“鄰域”概念,根據這一概念建立了抽象空間的完整理論,後人稱他建立的這種拓撲空間為豪斯多夫空間(即現在的T2拓撲空間)。同時期的匈牙利數學家裡斯還從導集出發定義了拓撲空間。20世紀20年代,原蘇聯莫斯科學派的數學家П.С.亞里山德羅夫與烏雷松等人對緊與列緊空間理論進行了系統研究,並在距離化問題上有重要貢獻。1930年該學派的吉洪諾夫證明了緊空間的積空間的緊性,他還引進了拓撲空間的無窮乘積(吉洪諾夫乘積)和完全正規空間(吉洪諾夫空間)的概念。
20世紀30年代後,法國數學家又在拓撲空間方面做出新貢獻。1937年布爾巴基學派的主要成員H.嘉當引入“濾子”、“超濾”等重要概念,使得“收斂”的更本質的屬性顯示出來。韋伊提出一致性結構的概念,推廣了距離空間,還於1940年出版了《拓撲群的積分及其套用》一書。1944年迪厄多內引進雙緊緻空間,提出仿緊空間是緊空間的一種推廣。1945年弗雷歇又提出抽象距的概念,他的學生們進行了完整的研究。布爾巴基學派的《一般拓撲學》亦對拓撲空間理論進行了補充和總結。
此外,美國數學家斯通研究了剖分空間的可度量性,1948年證明了度量空間是仿緊的等結果。捷克數學家切赫建立起緊緻空間的包絡理論,為一般拓撲學提供了有力工具。他的著作《拓撲空間論》於1960年出版。近幾十年來拓撲空間理論仍在繼續發展,不斷取得新的成果。
映射空間
亦稱函式空間。拓撲學的一個基本概念。一類重要的拓撲空間。設X,Y是集合,F為X到Y的映射組成的族。在F上引入拓撲使之成為拓撲空間,則稱F為映射空間。在映射空間理論中常見的拓撲有點態收斂拓撲、緊開拓撲、一致收斂拓撲、緊收斂拓撲等。
緊開拓撲
緊開拓撲是映射空間上一類常見的拓撲。設F為拓撲空間X到拓撲空間Y的映射族,若
W(K,U)={f∈F|f(K)U},
則以集族{W(K,U)|K為X的緊子集,U為Y的開集}為子基在F中生成的拓撲稱為F上的緊開拓撲。由於單點集為緊集,所以F上的緊開拓撲細於F上的點態收斂拓撲。若值域空間Y是豪斯多夫空間,則F上賦予緊開拓撲也是豪斯多夫空間。若Y是正則空間且F中每一元都是連續的,則F上賦予緊開拓撲也是正則空間。
一致結構
一致結構是集合上的一種結構。設X為集合,U為X×X的非空子集族。若U滿足下列條件,則稱U是X上的一致結構:
1.U的每一個元包含對角線Δ.
2.若U∈U,則U∈U,其中
U={(x,y)|(y,x)∈U}.
3.若U∈U,則存在V∈U使得V°VU,其中
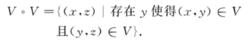 緊收斂拓撲
緊收斂拓撲4.若U,V∈U,則U∩V∈U.
5.若U∈U並且UVX×X,則V∈U.
具有一致結構U的集合X稱為一致空間,記為(X,U)。一致空間的概念是韋伊(Weil,A.)於1938年引入的。布爾巴基(Bourbaki,N.)於1940年首先給予系統的論述。圖基(Tukey,J.W.)於1940年用覆蓋族定義並研究了一致空間的等價的概念。艾斯貝爾(Isbell,J.R.)於1964年出版的書中,包含了用覆蓋敘述的一致空間理論的重要發展。一致空間也可用偽度量族來描述,它是由布爾巴基於1948年給出的。
