分組分解法
 分組分解法
分組分解法分組分解是因式分解的一種複雜的方法,讓我們來須有預見性。能預見到下一步能繼續分解。而“預見”源於細緻的“觀察”,分析多項式的特點,恰當的分組是分組分解法的關鍵。
套用分組分解法因式分解,不僅可以考察提公因式法,公式法,同時它在代數式的化簡,求值及一元二次方程,函式等學習中也有重要作用。
能分組分解的方程有四項或六項或大於六項,一般的分組分解有兩種形式:2+2分法,3+1分法。
例如:
2+2分法:
ax+ay+bx+by
=(ax+ay)+(bx+by)
=a(x+y)+b(x+y)
=(a+b)(x+y)
我們把ax和ay分一組,bx和by分一組,利用乘法分配律,兩兩相配,立即解除了困難。
同樣,這道題也可以這樣做。用另外兩個相同的來換:
ax+ay+bx+by
=(ax+bx)+(ay+by)
=x(a+b)+y(a+b)
=(a+b)(x+y)
3+1分法:
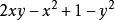 分組分解法
分組分解法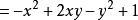 分組分解法
分組分解法 分組分解法
分組分解法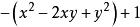 分組分解法
分組分解法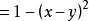 分組分解法
分組分解法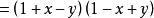 分組分解法
分組分解法難點
由於不同的題目有不同的需要,所以必須善於判斷分組方式並能靈活運用。
習題
下面我們來做幾道練習題:
1. 5ax+5bx+3ay+3by
解法:=5x(a+b)+3y(a+b)
=(5x+3y)(a+b)
說明:係數一樣可以做分組分解,和上面一樣,把5ax和5bx看成整體,把3ay和3by看成一個整體,利用乘法分配律輕鬆解出。
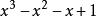 分組分解法
分組分解法2.
解法:=(x^3-x^2)-(x-1)
=x^2(x-1)-(x-1)
=(x-1)(x^2-1)
利用2+2分法,提公因式法提出x^2,然後相合輕鬆解決。
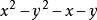 分組分解法
分組分解法3.
解法:=(x^2-y^2)-(x+y)
=(x+y)(x-y)-(x+y)
=(x+y)[(x-y)-1]
=(x+y)(x-y-1)
利用2+2分法,再利用公式法a^2-b^2=(a+b)(a-b),然後相合解決。
課後練習:
(1) 18a^2-32b^2-18a+24b
(2) x^2-25+y^2-2xy
(3) y^4-4y^3+4y^2-1
(4) 4a^2-b^2-4c^2+4bc
參考答案:
(1) 2(3a+4b-3)(3a-4b)
(2) (x-y+5)(x-y-5)
(3) (y^2-2y-1)(y-1)^2
(4)(2a +b-2c)(2a- b+2c)

