名詞解釋
同質分組
它是將一組研究對象分為相對同質的群組(clusters)。
通俗的講法,就是:物以類聚,人以群分。
集合論
 A-B的venn圖
A-B的venn圖在數學上,有一個基礎概念和它相似:
集合[aggregate]指一組具有某種
共同性質的數學元素。它是把人們的直觀的或思維中的某些確定的能夠區分的對象匯合在一起,使之成為一個整體(或稱為單體),這一整體就是集合。組成一集合的那些對象稱為這一集合的
元素(或簡稱為
元)。
康托(Cantor, G.F.P.,1845年—1918年,德國數學家先驅,是集合論的創始者。
外延公理對於任意的集合S1和S2,S1=S2若且唯若對於任意的對象a,都有若a∈S1,則a∈S2;若a∈S2,則a∈S1。一定範圍的,確定的,可以區別的事物,當作一個整體來看待,就叫做集合,簡稱集,其中各事物叫做集合的元素或簡稱元。
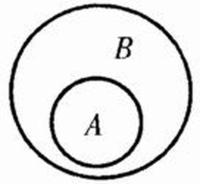 集合
集合1.確定性:每一個對象都能確定是不是某一集合的元素,沒有確定性就不能成為集合。
2.獨立性:集合中的元素的個數、集合本身的個數必須為自然數。
3.互異性:集合中任意兩個元素都是不同的對象,沒有重複。
4.無序性:{a,b,c}{c,b,a}是同一個集合。
5.純粹性:所謂集合的純粹性,用個例子來表示。集合A={x|x<2},集合A 中所有元素都要符合x<2,這就是集合純粹性。
6.完備性:仍用上例,所有符合x<2的數都在集合A中,即所謂完備性。
模糊集合
用來表達模糊性概念的集合。 又稱模糊集、模糊子集。狹義的集合是指具有某種屬性的對象的全體。這種屬性所表達的概念是清晰的,界限分明的。每個對象對於集合的隸屬關係也是明確的,非此即彼。但在人們的思維中還有著許多模糊的概念,它們所描述的對象屬性不能簡單地用“是”或“否”來回答,模糊集合就是指具有某個模糊概念所描述的屬性的對象的全體。由於概念本身不是清晰的、界限分明的,因而對象對集合的隸屬關係也不是明確的、非此即彼的。這一概念是美國加利福尼亞大學控制論專家L.A.扎德於 1965 年首先提出的。這一概念的出現使得數學的思維和方法可以用於處理模糊性現象,從而構成了模糊集合論的基礎。
概念延伸
聚類分析
在統計學上有個重要概念,叫做聚類。
聚類 是將數據或者對象分類到不同的類或者簇這樣的一個過程,所以同一個簇中的對象有很大的相似性,而不同簇間的對象有很大的相異性。聚類與分類的不同在於,聚類所要求劃分的類是未知的,它依據研究對象(樣品或指標)的特徵,對其進行集合分組,減少研究對象的數目。各類事物缺乏可靠的歷史資料,無法確定共有多少類別,目的是將性質相近事物歸入一類而各指標之間具有一定的相關關係。
聚類分析 (cluster analysis) 是一種將研究對象分為相對同質的群組(clusters)的統計分析技術,也叫分類分析或數值分類。聚類分析指將物理或抽象對象的集合分組成為由類似的對象組成的多個類的分析過程。它是一種重要的人類行為。聚類分析的目標就是在相似的基礎上收集數據來分類。聚類源於很多領域,包括數學,計算機科學,統計學,生物學和經濟學。在不同的套用領域,很多聚類技術都得到了發展,這些技術方法被用作描述數據,衡量不同數據源間的相似性,以及把數據源分類到不同的簇中。
從統計學的觀點看,聚類分析是通過數據建模簡化數據的一種方法。傳統的統計聚類分析方法包括系統聚類法、分解法、加入法、動態聚類法、有序樣品聚類、有重疊聚類和模糊聚類等,採用k-均值、k-中心點等算法的聚類分析工具已被加入到許多著名的統計分析軟體包中,如SPSS、SAS等。
從機器學習的角度講,簇相當於隱藏模式。聚類是搜尋簇的無監督學習過程。與分類不同,無監督學習不依賴預先定義的類或帶類標記的訓練實例,需要由聚類學習算法自動確定標記,而分類學習的實例或數據對象有類別標記。聚類是觀察式學習,而不是示例式的學習。
從實際套用的角度看,聚類分析是數據挖掘的主要任務之一。而且聚類能夠作為一個獨立的工具獲得數據的分布狀況,觀察每一簇數據的特徵,集中對特定的聚簇集合作進一步地分析。聚類分析還可以作為其他算法(如分類和定性歸納算法)的預處理步驟。以分層次管理的套用為例,聚類分析是通過數據挖掘來識別管理對象的層次,通過聚類觀察到管理對象的特徵,集中對特定層次的管理對象進行分析。此方法的主要步驟有:1.數據預處理;2.為衡量數據點間的相似度定義一個距離函式;3.聚類或分組;4.評估輸出。具體方法運用可藉助統計專業知識和人才,對管理對象和管理方法進行聚類分層。
主成分分析
主成分分析方法,首先是由K.皮爾森對非隨機變數引入的,爾後H.霍特林將此方法推廣到隨機向量的情形。其原理是:設法將原來變數重新組合成一組新的互相無關的幾個綜合變數,同時根據實際需要從中可以取出幾個較少的總和變數儘可能多地反映原來變數的信息的統計方法,也是數學上處理降維的一種方法。這一分析方法是將多個變數通過線性變換,選出較少個重要變數的一種多元統計分析方法。樣本信息的大小通常用離差平方和或方差來衡量。通常數學上的處理就是將原來P個指標作線性組合,作為新的綜合指標。最經典的做法就是用F1(選取的第一個線性組合,即第一個綜合指標)的方差來表達,即Var(F1)越大,表示F1包含的信息越多。因此在所有的線性組合中選取的F1應該是方差最大的,故稱F1為第一主成分。如果第一主成分不足以代表原來P個指標的信息,再考慮選取F2即選第二個線性組合,為了有效地反映原來信息,F1已有的信息就不需要再出現再F2中,用數學語言表達就是要求Cov(F1, F2)=0,則稱F2為第二主成分,依此類推可以構造出第三、第四,……,第P個主成分。
主要分析步驟如下:第一步,指標數據標準化(SPSS軟體自動執行);第二步,指標之間的相關性判定;第三步,確定主成分個數m;第四步,主成分Fi表達式;第五步,主成分Fi命名。
這一方法在分層次管理套用上,可藉助IT技術對數據進行處理,能更有效地做出信息判斷,分劃出管理對象和管理方法的層次。在管理對象的差異分析時,往往會提出很多與此有關的變數,統計分析方法能從太多變數個數中,找出變數個數較少而得到的信息較多結果。
因子分析
因子分析法是研究從變數群中提取共性因子的統計技術,最早由英國心理學家C.E.斯皮爾曼提出。他發現學生的各科成績之間存在著一定的相關性,一科成績好的學生,往往其他各科成績也比較好,從而推想是否存在某些潛在的共性因子,或稱某些一般智力條件影響著學生的學習成績。因子分析可在許多變數中找出隱藏的具有代表性的因子,將相同本質的變數歸入一個因子,可減少變數的數目,還可檢驗變數間關係的假設。
因子分析與主成分分析有很大的不同,主成分分析不能作為一個模型來描述,它只能作為一般的變數變換,主成分是可測的原始變數的線性組合,而因子分析需要構造一個因子模型,公共因子一般不能表示為原始變數的線性組合。因子分析的基本思想是根據變數相關性的大小把變數分組,使得同組內的變數之間相關性較高,但不同組內的變數的相關性較低.每組變數代表一個基本結構,這個基本結構稱為公共因子。對於所研究的問題,就可以試圖用最少個數的不可觀測的所謂公共因子的線性函式與特殊因子之和來描述原來觀測的每一個分量。因子分析可用於對變數或樣品的分類處理。可根據因子的得分值,在因子軸所構成的空間中把變數或樣品構畫出來,形象直觀地達到分類的目的。研究變數的相互關係的因子分析稱為R型因子分析,而研究樣品之間的相互關係的因子分析稱為Q型因子分析。
以人力資源管理為例,如2家公司對48名應聘者進行面試,並給出他們在15個方面所得的分數。這15個方面是:申請書的形式、外貌、專業能力、討人喜歡、自信心、精明、誠實、推銷能力、經驗、積極性、抱負、理解能力、潛力、交際能力和適應性。通過因子分析,可把這15個方面歸結為應聘者的外露能力、討人喜歡的程度、經驗、專業能力和外貌這五個因子,為選用人才提供了差異性識別方法。在實際套用中,通過因子得分可以得出不同因子的重要性指標,而管理者則可根據這些指標的重要性來決定首先管理對象的分層和相應層次的管理對策。
實驗實例
對比實驗
心理學實驗設計的主要步驟可歸納為:
1.建立與研究假說有關的統計假說;
2.確定實驗中使用的實驗處理(自變數)和必須控制的多餘條件(額外變數);
3.確定實驗中需要的實驗單元(被試)的數量及被試抽樣的總體;
4.確定將實驗條件分配給被試的方法;
5.確定實驗中每個被試要記載的測量(因變數)和使用的統計分析。
實驗設計的主要功用是對變數的控制,首先是在控制條件下有效地操縱或改變自變數,使因變數(即反應變數)的變化得到觀察。例如,研究兩種教學方法對兒童學業成就的影響時,實驗設計者應安排使其他條件儘量相同,即保證被試的,如選擇家庭和學校環境相似、學業基礎相似,年齡相同的兩組兒童,只控制使用兩種不同的教學方法,然後考查二者對學習結果的影響。
對比設計
這是心理實驗最基本的設計之一。它把被試分為兩組,一組為實驗組,施以實驗處理(也稱處理);
另一組為控制組,不加實驗處理。為使兩組被試儘量同質,便於比較,一般採用隨機分派法分組,通過測量兩組的差異檢驗實驗處理的效果。
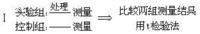 同質分組
同質分組其基本模式如Ⅰ。
即使隨機分派被試,但樣本不很大時,也很難保證兩組在處理前同質,因而兩組測量的差異不一定全是處理的結果。為了彌補這一不足,常在處理前先對兩組進行測量,即模式Ⅱ。
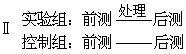 同質分組
同質分組如果前測的結果相近,可直接比較兩組的後測,並用t檢驗法檢驗其差異,這時的差異即可認為完全是由處理造成的。如果兩個前測不同,就要把前測作為共變數,進行獨立樣本單因素的共變數分析。這種設計的優點是克服了大部分影響內在效度的無關變數。但由於有前測,又增加了前測的反作用效果,使外在效果有所降低。所謂測驗的反作用效果是指處理前進行的前測可能增加或減少被試對處理的敏感性。
正確的實驗設計在於合理安排實驗程式,對無關變數進行有效的控制。心理學實驗中的無關變數,有些可以象理化實驗那樣通過一定的實驗儀器及技術予以排除,但大部分難以排除,必須依靠實驗設計平衡或抵消其影響。這種控制方法稱作實驗控制法(實驗誤差)。還有一些無關變數,雖然明知它對結果有影響,但限於實驗條件,不可能用實驗控制法加以平衡或抵消,而只能在實驗結束後,用統計的方法分析出來,從結論中排除,叫做統計控制法(統計誤差)。評價一個實驗設計主要是看其能否:①恰當地解決研究者所要解決的問題,即實驗設計必須與研究問題匹配;②有較好的“內在效度”,即能夠有效地控制無關變數,使反應變數的變化完全由自變數決定;③實驗結果應具有一定的科學性、普遍性,能夠推論到其他被試或其他情境,即有較高的“外在效度”。
套用
目前,同質分組在政治、學術、金融、教育、網際網路、市場分析、遊戲娛樂、犯罪預防 等諸多領域都有廣泛的套用。
生物學
用於動植物分類和對基因進行分類識別,獲取對種群固有結構的認識,以及對生理學、病理學、基因組的研究。
地理學
能夠幫助發現被觀察的地理數據互相之間的相似性,包括天文、水文、氣象資料的分析。
商業分析
它被用來發現不同的客戶群,並且通過購買模式刻畫不同的客戶群的特徵。它是細分市場的有效工具,同時也可用於研究消費者行為,尋找新的潛在市場、選擇實驗的市場,並作為多元分析的預處理。
金融
通過一個高的平均消費來鑑定汽車保險單持有者的分組,同時根據住宅類型,價值,地理位置、升值潛力來鑑定一個城市的房產分組。
網際網路
被用來在網上進行文檔歸類來修覆信息。
電子商務
在電子商務中網站建設數據挖掘中也是很重要的一個方面,通過分組聚類出具有相似瀏覽行為的客戶,並分析客戶的共同特徵,可以更好的幫助電子商務的用戶了解自己的客戶,向客戶提供更合適的服務。
