正文
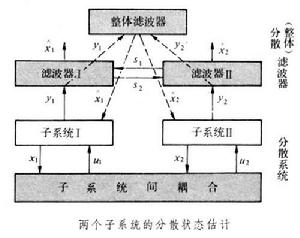
對分散系統中受噪聲干擾的狀態量在一定的統計意義下作出最優估計的信息處理技術，簡稱分散狀態估計或分散卡爾曼濾波。對含有隨機擾動和測量噪聲的分散系統進行控制,要解決兩個問題：一是狀態估計,一是最優控制。對於這類系統用集中的方法進行狀態估計和最優控制是有困難的。通常是把大系統分解為若干子系統用分散的方法解決。這就出現了分散狀態估計問題。在有些要求進行狀態估計的套用場合，用整體卡爾曼濾波時要求的計算量過大，集中信息有實際困難，可以人為地將問題轉換為分散濾波來解決。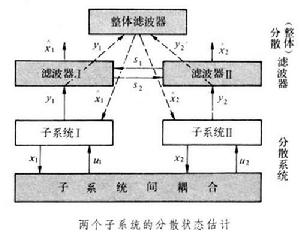
受噪聲干擾的狀態量是個隨機量，不可能測得精確值，但可對它進行一系列觀測，並依據一組觀測值，按某種統計觀點對它進行估計。使估計值儘可能準確地接近真實值，這就是最優估計。真實值與估計值之差稱為估計誤差。若估計值的數學期望與真實值相等，這種估計稱為無偏估計。估計值的方差越小，表示估計值取其數學期望的機率越大。因此，分散系統狀態估計問題就是：設計一個分散濾波器，它由若干個局部濾波器組成，每一局部濾波器均有自已的輸入，要求確定各局部濾波器的輸出，使某種整體的性能指標為最小（見圖）。圖中局部濾波器的輸入y包括系統模型數據和線上測量數據。局部濾波器的輸出 憫即為狀態估計，它是無偏估計。x為狀態量，u為從其他子系統來的耦合量。圖為兩個子系統的情況。通常，人們常用估計誤差的方差作為整體的性能指標。 所選用的濾波器的信息結構不同就構成不同的濾波器。信息結構是完全集中模式時,對應的濾波器稱為整體卡爾曼濾波器。這時沒有信息流的約束，可利用系統模型和線上信息的全部數據，因而濾波性能最好。性能指標值記為JG。但除非確能實現集中模式，否則它只能作為與其他型式濾波器進行比較的標準。當信息結構是完全分散時,對應的濾波器稱為確實局部無偏濾波器。這時只採用描述本子系統模型的信息和線上信息，各局部濾波器之間沒有信息交換。這種濾波器的結構簡單，要求的信息量最少。但濾波性能因缺少整體信息而下降。性能指標值記為JSLU。當局部濾波器可使用整體系統模型信息但只能用本局部濾波器線上信息時，對應的濾波器稱為局部化整體動態濾波器。這種濾波器因使用整體模型信息，性能較好，但濾波器複雜，不易實現，而且需要有一個大容量的資料庫，用以存儲整體系統模型的數據。性能指標記為JLGD。一種較可取的信息結構是允許局部濾波器之間有部分信息交換(圖中用s表示),即在確實局部無偏濾波器的基礎上擴充各局部濾波器占有的信息，互相交換彼此的輸入和輸出值。對應的濾波器稱為擴充確實局部無偏濾波器。這樣既能基本上保持確實局部無偏濾波器的結構簡單,又能適當改善濾波性能。性能指標記為JESLU。比較上面四種濾波器的性能可得JG≤JLGD≤JSLU，JG≤JESLU≤JSLU。至於選擇JLGD還是JESLU，則取決於系統的特點和擴充時提出的特定要求。
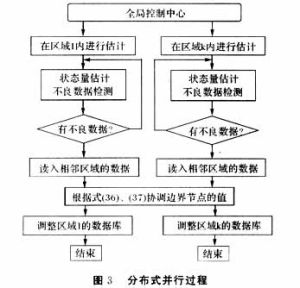分散系統