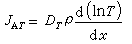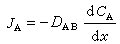分子擴散
以濃度差為推動力的擴散，即物質組分從高濃度區向低濃度區的遷移，是自然界和工程上最普遍的擴散現象；以溫度差為推動力的擴散稱為熱擴散；在電場、磁場等外力作用下發生的擴散，則稱為強制擴散。在化工生產中，物質在濃度差的推動下在足夠大的空間中進行的擴散最為常見，一般分子擴散就指這種擴散，它是傳質分離過程的物理基礎，在化學反應工程中也占有重要地位。此外，還經常遇到流體在多孔介質中的擴散現象，它的擴散速率有時控制了整個過程的速率，如有些氣固相反應過程的速率。至於熱擴散只在穩定同位素和特殊物料的分離中有所套用，強制擴散則套用甚少。
斐克定律 1855年德國人A.E.斐克提出描述分子擴散規律的基本定律。在組分A和B的混合物中,組分A的擴散速率（也稱擴散通量）,即單位時間內組分A通過垂直於濃度梯度方向的單位截面擴散的物質量為：
JA=－DABΔCA
式中負號表示物質A向濃度減小的方向傳遞;DAB為組分A在組分B中的分子擴散係數;ΔCA為濃度CA的梯度。如果CA僅沿x方向變化，則簡化為：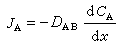
多孔介質中的擴散 物質在多孔介質中的擴散，根據孔道的大小、形狀以及流體的壓強不同分為三類情況（見圖）。
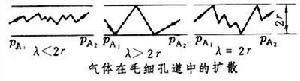①容積擴散。當毛細管孔道直徑遠大於分子平均自由程 憳，即(憳/2r)≤(1/100)（r為毛細孔道的平均半徑）時，在分子的運動中主要發生分子與分子間的碰撞，分子與管壁的碰撞所占比例很小。其擴散機理與分子擴散相同，故也稱分子擴散。孔內所含流體的分子擴散，仍可用斐克定律來計算；只需考慮多孔介質的空隙率ε和曲折因數τ（表示因毛細孔道曲折而增加的擴散距離），對一般的分子擴散係數加以修正。此時有效擴散係數為：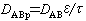 
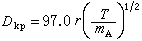
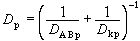
熱擴散 溫度梯度加於靜止的氣體或液體混合物時，一種分子趨向高溫區，另一種趨向低溫區，從而在混合物內產生濃度梯度，這種現象又稱為沙萊特效應。在兩組分混合物中，給定組分A的熱擴散通量用下式表示：
