計算
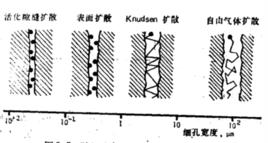
如果氣體密度不大、多孔固體介質的孔徑較小,則氣體分子平均自由程可能遠大於介質的孔徑,此時氣體分子與介質孔壁碰撞的機會多於分子之間的碰撞,阻止氣體擴散的主要因素為氣體分子與孔壁的碰撞,而分子之間的碰撞阻力可以忽略不計,我們把這種條件下的擴散稱為Knudsen擴散。
根據氣體分子運動學說,氣體分子通過圓柱形微孔的Knudsen擴散係數D(cm /s),可以按下式計算:
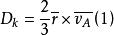 克努森擴散
克努森擴散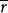 克努森擴散
克努森擴散式中,-微孔的平均半徑,cm;
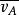 克努森擴散
克努森擴散-氣體分子A的均方根速度,cm/s,可按下式計算:
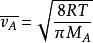 克努森擴散
克努森擴散將其代入(1)式有:
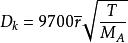 克努森擴散
克努森擴散式中,M-氣體分子A的分子量;
T-絕對溫度,K。
因為在低壓下各種氣體分子之間的碰撞可以忽略,故此式適用於體系中存在的任何組分。
如果考慮到氣體分子在多孔固體介質中實際擴散截面積的較少和擴散路徑的增大,則同樣需要對Knudsen擴散係數進行校正:
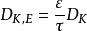 克努森擴散
克努森擴散式中,D-有效Knudsen擴散係數。
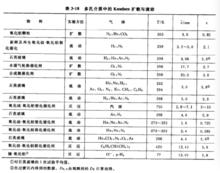
對於一些在較低溫度下以Knudsen擴散為主的體系,表中列出根據實驗結果計算出來的曲折度。
 多孔介質中的Knudsen擴散與流動
多孔介質中的Knudsen擴散與流動在某些條件下,分子之間的碰撞和分子與孔壁之間的碰撞都起作用,此時總的擴散速率與分子擴散Knudsen擴散均有關係,我們把這種擴散稱為混合擴散(mixed diffusion)。在這種情況下,有效擴散係數D。可以近似地表示為:
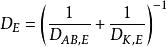 克努森擴散
克努森擴散判斷
判斷擴散過程以哪種擴散為主
判斷擴散過程是以Knudsen擴散為主,還是以分子擴散為主,通常有兩種方法。
 克努森擴散
克努森擴散第一種方法是比較D和D的大小。如果,則過程速率的限制步驟為Knudsen擴散;反之,則為分子擴散。
第二種方法是首先計算出氣體分子的平均自由程:
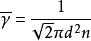 克努森擴散
克努森擴散式中,d-分子的碰撞直徑,cm;
n-分子的密度,cm 。
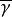 克努森擴散
克努森擴散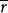 克努森擴散
克努森擴散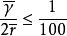 克努森擴散
克努森擴散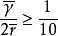 克努森擴散
克努森擴散將計算的與孔徑作比較,如果,則為分子擴散;如果,則為Knudsen擴散。
關係
分子擴散係數和努森擴散係數的關係
套用氣體動力學理論,可以導出下式:
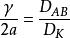 克努森擴散
克努森擴散式中,A-分子的平均自由程,cm。
該式表明,γ對2a的比值等於分子擴散係數D和努森擴散係數D之比。由此可以確定在某一擴散過程中,是否可以忽略分子擴散係數式或努森擴散係數。很明顯,在壓力或分子濃度上升時,將發生從努森擴散向分子擴散的轉化。