溶液中離子的擴散

溶液中離子的擴散

正文

擴散是溶液的基本性質，是微粒（分子、原子）的熱運動而產生的物質遷移現象，主要由濃差、溫差和湍流運動引起，研究擴散可為溶液結構提供信息。
液體擴散的基本公式是斐克定律：

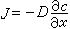
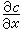式中J為物質的通量,即單位時間內通過單位面積的物質量；D是擴散係數；是濃度梯度。
電解質溶液的擴散　兩組分體系中的擴散　在單組分體系中，自擴散係數用D*表示；在兩組分體系中用D奮和D奯表示。在非理想情況下，D奯為濃度的函式，如果忽略粘度η對淌度U的影響，則有：

式中D凁為c →0時的D奯；ab為活度；cb為濃度；xb為摩爾分數；yb為摩爾活度係數。由於組分i的淌度 Ui是單位力影響下組分i所獲得的平均漂移速度,或簡單地認為是摩擦係數f的倒數,根據斯托克斯定律f=6πηr（r為粒子半徑），則U與1/η成正比，在考慮η變化時,上式可寫成：

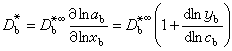
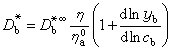
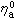式中為純組分a的粘度。
單電解質的擴散　在電解質溶液中，極限當量電導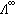與擴散係數D+、D_之間的關係可用能斯脫－愛因斯坦公式表達：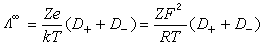

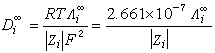
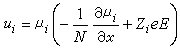
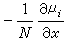式中Z為離子的電荷數；e為電子的電荷數;k為玻耳茲曼常數；T為熱力學溫度;F為法拉第常數；R為氣體常數。當c→0時，上式可簡化為：

在電解質溶液中，電中性要求正、負離子都以同樣的速率移動，因此，對於電解質從整體上說存在著一個擴散係數Db。在x方向的某一離子的擴散速度ui為：

式中為粒子i在x方向的驅動力；μi為粒子i的化學勢；N 為阿伏加德羅數；ZieE為在電場E的存在下，帶電荷Zie的離子i遭受到的力。對於正和負離子，這個擴散速度都應該是同樣的，從式 u+＝u-消除E，並套用v+Z++v-Z-＝0的關係，可得：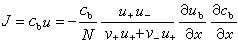

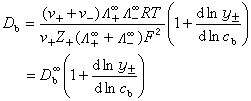
式中J為溶質通量;v+和v-為正負離子個數。將上式與斐克定律相比，得：

式中y±為平均體積摩爾活度係數,此式稱為能斯脫－哈脫萊方程。
電泳效應對擴散的影響　在電導中，離子互相吸引產生兩種效應：一是鬆弛效應，即外電場的影響使對稱的離子氛轉化為非對稱的；另一種是電泳效應，即在外電場的影響下溶劑分子和離子作反向的對流。在單獨電解質的擴散里，兩種離子以相同速率向前推進，離子氛的對稱性仍能維持，因而沒有鬆弛效應，但是電泳效應仍然存在，因為離子移動時穿過溶劑，而溶劑分子的擴散方向是相反的。這個效應與電解質的濃度有關，對稱電解質從無限稀到濃度c時，可得到：

這些效應引起Db的改正為墹1+墹2,它只有電導率相應的改正值的1/10。
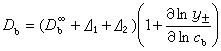
締合式電解質對擴散的影響　離子締合對擴散的影響是降低微粒的阻力。因為在液體中移動時，一個微粒的阻力總比兩個小些，結果擴散速度上升。在稀溶液中得到下式：

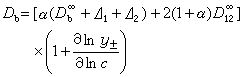
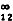式中 α為電離度；D為無限稀釋溶液中一個離子對的擴散係數，濃度為0.001～0.005摩爾／千克時D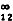是常數。
互擴散對擴散的影響　在兩組分體系中,當B擴散到右邊時，為使體系平衡，必然有一些物質流到左邊，因此淨效應可被描述為與方向中的整體運動結合的 B的純擴散。在這種情況下，用單個擴散係數Dab來描述通過擴散的任一組分的濃度變化，就叫做互擴散係數。假設體積與組成無關時，Dab即為：

式中xa、xb為組分a、b的摩爾分數;fb為組分b的有理活度係數，此式稱為吉布斯－杜亥姆擴散方程，它還可表述為：

式中已假設u與η成反比關係。
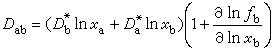
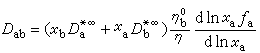
自擴散　純液體分子從一點移動到另一點的運動稱為自擴散。在溶液中實際能實現的是示蹤擴散，例如極少量的放射性 Na*離子在氯化鈉中的擴散。因為 Na*離子的濃度很小，基本無反向溶劑流動，所以電泳效應可以忽略。定量的方程為：

D凂可由能斯脫－愛因斯坦公式計算。
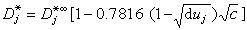
濃溶液的擴散　必須考慮溶劑的移動、溶液的粘度和離子的水化。非電解質濃溶液的擴散公式為：

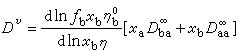
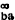式中xa和xb為溶劑a和溶質b的摩爾分數;D和D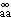分別為b在無限稀釋下的擴散係數和純溶劑的擴散係數；Dv為兩組分體系的分體積不變時的擴散係數。
把上式用於單電解質在濃溶液中的擴散，得出高濃度下水化電解質的擴散公式：

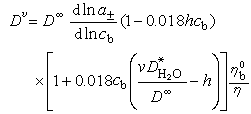
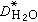式中h為電解質水化數。對電解質的體積濃度來說,水化和非水化並無區別,因此Dv即為無水的擴散係數D,為純水的擴散係數,對1:1價態的電解質,離子個數v＝2。上式能符合許多1:1價態的鹽,濃度可達1摩爾／千克,誤差約為0.5％。
參考書目
　黃子卿：《電解質溶液理論導論》，科學出版社，北京，1964。

配圖

相關連線