簡介
凸最佳化,或叫做 凸最最佳化, 凸最小化,是數學最最佳化的一個子領域,研究定義於凸集中的凸函式最小化的問題。凸最佳化在某種意義上說較一般情形的數學最最佳化問題要簡單,譬如在凸最佳化中局部最優值必定是全局最優值。凸函式的凸性使得凸分析中的有力工具在最最佳化問題中得以套用,如次導數等。
凸最佳化套用於很多學科領域,諸如自動控制系統,信號處理,通訊和網路,電子電路設計,數據分析和建模,統計學(最最佳化設計),以及金融。在近來運算能力提高和最最佳化理論發展的背景下,一般的凸最佳化已經接近簡單的線性規劃一樣直捷易行。許多最最佳化問題都可以轉化成凸最佳化(凸最小化)問題,例如求凹函式 f最大值的問題就等同於求凸函式 - f最小值的問題。
凸函式
 凸最佳化
凸最佳化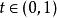 凸最佳化
凸最佳化凸函式是一個定義在某個向量空間的凸子集C(區間)上的實值函式f,如果在其定義域C上的任意兩點,以及,有
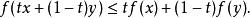 凸最佳化
凸最佳化也就是說,一個函式是凸的若且唯若其上境圖(在函式圖像上方的點集)為一個凸集。
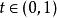 凸最佳化
凸最佳化如果對於任意的有
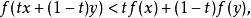 凸最佳化
凸最佳化函式f是 嚴格凸的。
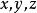 凸最佳化
凸最佳化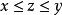 凸最佳化
凸最佳化若對於任意的,其中,都有
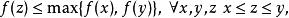 凸最佳化
凸最佳化則稱函式f是 幾乎凸的。
舉例
以下問題都是凸最佳化問題,或可以通過改變變數而轉化為凸最佳化問題:
•最小二乘
•線性規劃
•線性約束的二次規劃
•半正定規劃
方法
凸最佳化(凸最小化)問題可以用以下幾種方法求解:
•捆集法
•次梯度法
•內點法
凸最大化
通常凸最佳化的定義要求目標函式 f在可行域內被最小化,而在某些的線性規劃問題中也會研究最大化。
