介紹
凸集的邊界總是凸曲線。 包含歐幾里得空間的給定子集A的所有凸集的交集稱為A的凸包。它是包含A的最小凸集。凸函式是在具有其epigraph（函式圖上或上方的點集合）為凸集的屬性的間隔上定義的實值函式。 凸最小化是一個最佳化的子領域，研究了凸函式在凸集上的最小化問題。 用於凸集和凸函式屬性研究的數學分支稱為凸分析。
在向量空間
凸集
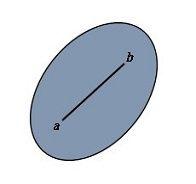
凸集令S是實數上的向量空間，或者更一般地，是在某個有序域上，這包括歐幾里德空間。如果對於C中的所有x和y，並且在區間（0,1）中的所有t，點 也屬於C，則S中的集合C被稱為凸。換句話說，連線x和y的線段上的每個點都在C中。這意味著實際或複雜拓撲向量空間中的凸集是路徑連線的。此外，如果除了端點之外的連線x和y的線段上的每個點都在C的內部，則C是嚴格凸起的。
R的凸子集（實數集）僅僅是R的間隔。歐幾里得平面的凸子集的一些例子是實心的正多邊形，實心三角形和實心三角形的交集。歐幾里德三維空間的凸子集的一些例子是阿基米德固體和柏拉圖式固體。克卜勒 - 波諾索多面體是非凸集的例子。
非凸集
不凸的集合稱為非凸集。 一個不是凸多邊形的多邊形有時被稱為凹多邊形，一些來源更普遍地使用術語凹集來表示非凸集，但大多數許可權禁止這種使用。
凸集的補集有時被稱為反凸集，特別是在數學最佳化的上下文中。
屬性
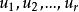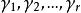凸集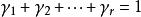
凸集
凸集如果S是n維空間中的凸集，則對於S中的任何r> 1，n維向量 的集合，對於任何非負數 ， 那 ，那么：
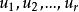凸集 凸集這種類型的向量被稱為 的凸組合。
一般的：
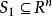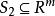凸集
凸集令和是凸集，則有以下重要性質：
凸集(1) 交集為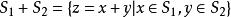凸集。
凸集(2) 和集為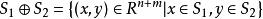凸集。
凸集(3) 直和為凸集。
交叉和聯合
向量空間的凸子集的集合具有以下屬性：
（1）空集和整個向量空間是凸的。
（2）任意凸集集合的凸點是凸的。
（3）凸子集的非遞減序列的並集是凸集。 對於凸集的非遞減序列的聯合的前述屬性，對嵌套集的限制很重要：兩個凸集的並集不必是凸的。
封閉凸集
閉合凸集是包含其所有極限點的凸集。 它們可以被表征為閉合半空間（位於超平面的一側上的空間中的點集合）的交集。
從剛才所說的，很明顯這樣的交叉是凸的，它們也是封閉的。 為了證明相反，即每個凸集可以表示為這樣的交集，需要以對於給定的閉凸集C和其外的點P的形式的支持超平面定理，存在封閉的半空間H，其包含 C而不是P.支持超平面定理是功能分析的哈恩 - 巴拿赫定理的特殊情況。
總和
凸包
矢量空間的每個子集A包含在最小的凸集（稱為A的凸包）中，即包含A的所有凸集的交集。凸包運算符Conv（）具有包集的特徵屬性：
一般的：S⊆Conv（S）；
不減少S⊆T意味著Conv（S）⊆Conv（T）和冪等於Conv（Conv（S））= Conv（S）。
凸集運算是需要的一組凸集合形成一個格子，其中“連線”操作是兩個凸集合的凸包的凸包
Conv（S）∨Conv（T）= Conv（S∪T）= Conv（Conv（S）∪Conv（T））
任何一組凸集合的集合本身都是凸的，所以（實數或複合）向量空間的凸子集形成一個完整的格線。
閔可夫斯基加法
在實際向量空間中，將兩個（非空）集合S1和S2的閔可夫斯基之和定義為通過向量元集合中的向量集合形成的集合S1 + S2：
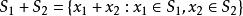凸集更一般地，有限族（非空）集合的閔可夫斯基和是通過元素向量的向量
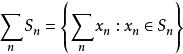凸集對於閔可夫斯基加法，僅包含零向量0的零集合{0}具有特殊的重要性：對於向量空間的每個非空子集S
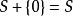凸集在代數術語中，{0}是閔可夫斯基加法的本體元素（在非空集合的集合上）。
閔可夫斯基加法和凸包
閔可夫斯基加法在獲得凸包的操作方面表現良好，如以下命題所示：
令S，S為真實矢量空間的子集，其閔可夫斯基和的凸包是其凸包的閔可夫斯基和：
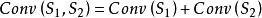凸集對於非空集合的每個有限集合，此結果更為一般：
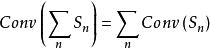凸集在數學術語中，閔可夫斯基求和和形成凸包的操作是相關聯的操作。
閔可夫斯基凸集合：
閔可夫斯基的兩個緊湊凸集的和是緊湊的。 緊湊凸集和閉合凸集合的總和是閉合的。
