定義
⒈對於一個集合D,D中任意有限個點的凸組合的全體稱為D的凸包。
⒉對於一個集合D,所有包含D的凸集之交稱為D的凸包。
可以證明,上述兩種定義是等價的
概念
 示例圖(一)
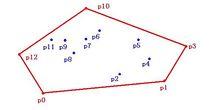
示例圖(一)1 點集Q的凸包(convex hull)是指一個最小凸多邊形,滿足Q中的點或者在多邊形邊上或者在其內。右圖中由紅色線段表示的多邊形就是點集Q={p0,p1,...p12}的凸包。
2 一組平面上的點,求一個包含所有點的最小的凸多邊形,這就是凸包問題了。這可以形象地想成這樣:在地上放置一些不可移動的木樁,用一根繩子把他們儘量緊地圈起來,並且為凸邊形,這就是凸包了。
 凸包
凸包數學定義:設S為歐幾里得空間 的任意子集。包含S的最小凸集稱為S的凸包,記作conv(S)。
平面求法
常見求法
凸包最常用的凸包算法是Graham掃描法和Jarvis步進法
Graham's Scan法
這個算法是由數學大師葛立恆(Graham)發明的,他曾經是美國數學學會(AMS)主席、AT&T首席科學家以及國際雜技師協會(IJA)主席。
問題
給定平面上的二維點集,求解其凸包。
過程
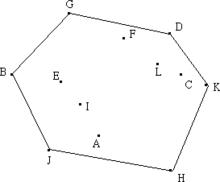
⒈ 在所有點中選取y坐標最小的一點H,當作基點。如果存在多個點的y坐標都為最小值,則選取x坐標最小的一點。坐標相同的點應排除。然後按照其它各點p和基點構成的向量<H,p>;與x軸的夾角進行排序,夾角由大至小進行順時針掃描,反之則進行逆時針掃描。實現中無需求得夾角,只需根據餘弦定理求出向量夾角的餘弦值即可。以下圖為例,基點為H,根據夾角由小至大排序後依次為H,K,C,D,L,F,G,E,I,B,A,J。下面進行逆時針掃描。
 示例圖(二)
示例圖(二)⒉ 線段<H,K>;一定在凸包上,接著加入C。假設線段<K,C>;也在凸包上,因為就H,K,C三點而言,它們的凸包就是由此三點所組成。但是接下來加入D時會發現,線段<K,D>;才會在凸包上,所以將線段<K,C>;排除,C點不可能是凸包。
 凸包
凸包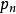 凸包
凸包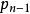 凸包
凸包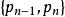 凸包
凸包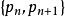 凸包
凸包⒊ 即當加入一點時,必須考慮到前面的線段是否在凸包上。從基點開始,凸包上每條相臨的線段的鏇轉方向應該一致,並與掃描的方向相反。如果發現新加的點使得新線段與上線段的鏇轉方向發生變化,則可判定上一點必然不在凸包上。實現時可用向量叉積進行判斷,設新加入的點為,上一點為,再上一點為。順時針掃描時,如果向量與的叉積為正(逆時針掃描判斷是否為負),則將上一點刪除。刪除過程需要回溯,將之前所有叉積符號相反的點都刪除,然後將新點加入凸包。
在上圖中,加入K點時,由於線段<H,C>要鏇轉到<H,K>的角度,為順時針鏇轉,所以C點不在凸包上,應該刪除,保留K點。接著加入D點,由於線段<K,D>要鏇轉到<H,K>的角度,為逆時針鏇轉,故D點保留。按照上述步驟進行掃描,直到點集中所有的點都遍歷完成,即得到凸包。
複雜度
這個算法可以直接在原數據上進行運算,因此空間複雜度為O⑴。但如果將凸包的結果存儲到另一數組中,則可能在代碼級別進行最佳化。由於在掃描凸包前要進行排序,因此時間複雜度至少為快速排序的O(nlgn)。後面的掃描過程複雜度為O(n),因此整個算法的複雜度為O(nlgn)。
Jarvis步進法
對於一個有三個或以上點的點集Q,過程如下:
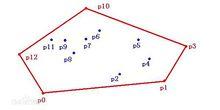 示例圖(三)
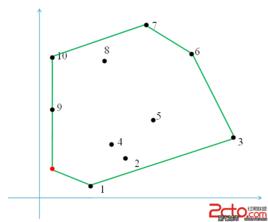
示例圖(三)計算點集最右邊的點為凸包的頂點的起點,如上圖的P3點。
Do
For i = 0 To 總頂點數
計算有向向量P3->Pi
If 其餘頂點全部在有向向量P3->Pi的左側或右側,則Pi點為凸包的下一頂點
Pi點加入凸包列表
GoTo 1
End If
Next
Exit Do
1:
Loop
此過程執行後,點按極角自動順時針或逆時針排序,只需要按任意兩點的次序就可以了。而左側或右側的判斷可以用前述的矢量點積性質實現。
中心法
先構造一個中心點,然後將它與各點連線起來,按斜率遞增的方法,求出凸包上部;再按斜率遞減的方法,求出凸包下部。
水平法
從最左邊的點開始,按斜率遞增的方法,求出凸包上部;再按斜率遞減的方法,求出凸包下部。水平法較中心法減少了斜率無限大的可能,減少了代碼的複雜度。
快包法
選擇最左、最右、最上、最下的點,它們必組成一個凸四邊形(或三角形)。這個四邊形內的點必定不在凸包上。然後將其餘的點按最接近的邊分成四部分,再進行快包法(QuickHull)。
代碼實例
C代碼一
C代碼二
Pascal代碼三