典型域

典型域(classical domain)是多複變函數論的基本概念。C中不可分解對稱有界域在全純等價下分類的標準域稱為典型域，它們有四大類和兩個特殊的域，分別在16維及27維復歐氏空間中，這兩個域也稱為例外典型域。

第一類典型域

第一種是m行n列的矩陣雙曲空間，它是由m行n 列的復元素矩陣Z並且適合於條件

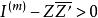典型域

典型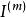域

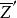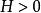典型域

典型域

的所組成，此處 表示m行列的單位方陣， 表示由Z行列互換並取共軛複數所得出的矩陣，因此它是n 行m列的。如果H是一個Hermite 方陣，則以 表示H是定正的。

第二類典型域

第二種是n 行列的對稱方陣的雙曲空間，它是由n 行列的復元素對稱方陣Z並且適合於條件

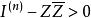典型域

的所組成。

第三類典型域

第三種是n 行列的斜對稱方陣的雙曲空間，它是由n 行列的復元素斜對稱方陣Z並且適合於條件

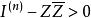典型域

的所組成。

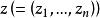第四類典型域

典型域

第四種可以稱為Lie球雙曲空間，它是由n(>2)維復元素矢量 並且適合於諸條件

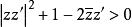典型域

及

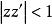典型域

的所組成。

相關介紹

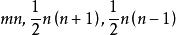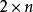典型域

典型域

這四種域的維數(複數維)各為 及n。最後一種，也可以表成為 實元素矩陣的雙曲空間。可遞的不可分解的囿對稱域僅有六種可能性，除以上的四種之外還有兩種，其一是16 維的某一種空間，另一是27維的某一種空間，從維數可以看出這兩種域是異常特殊的。