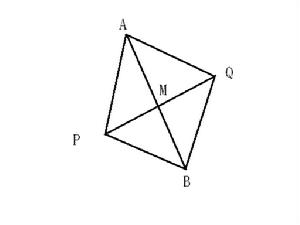
證明
在直線AB上取點N,使MN=AB,則PAB面積=PMN面積
QAB面積=QMN面積
故PAB面積/QAB面積=PMN面積/QMN面積=PM/QM
證明2
PAM與QAM高相等，所以PAM與QAM面積比等於PM與QM的長度比，同理PBM與QBM面積比等於PM與QM長度比，由此可證PAB面積/QAB面積=PM/QM
相關詞條
-
梅涅勞斯定理
梅涅勞斯（Menelaus）定理（簡稱梅氏定理）最早出現在由古希臘數學家梅涅勞斯的著作《球面學》（）中。 任何一條直線截三角形的各邊或其延長線，都使得三...
定理定義 定理證明 定理意義 -
塞瓦定理
塞瓦定理是指在△ABC內任取一點O，延長AO、BO、CO分別交對邊於D、E、F，則 (BD/DC)×(CE/EA)×(AF/FB)=1。 塞瓦(Giov...
驗證推導 定理推廣 數學意義 記憶方法 -
牛頓定理
特指平面幾何中的牛頓定理（Newton's Theorem） 牛頓線：和完全四邊形四邊相切的有心圓錐曲線的心的軌跡是一條直線,是完全四邊形三條對角線中點...
定理1 定理2 定理3 -
燕尾定理
燕尾定理：在三角形ABC中，AD，BE，CF相交於同一點O，有 S△AOB∶S△AOC=BD∶CD S△AOB∶S△COB=AE∶CE S△BOC∶S△...
驗證推導 定理推廣 -
高斯線定理
高斯線定理：四邊形ABCD中，直線DA與直線CB交於K，直線BA與直線CD交於L，N、M分別為AC、BD的中點，NM交KL與P.則P是KL中點
概念 證明 -
梅氏定理
梅氏定理，即梅涅勞斯（Menelaus）定理。其核心內容是關於三角形的。
梅氏定理 定理證明 逆定理證明 其他相關領域 -
梅尼勞斯定理
數學定理，簡稱梅氏定理，是由古希臘數學家梅涅勞斯首先證明的。使用梅涅勞斯定理可以進行直線形中線段長度比例的計算，其逆定理還是可以用來解決三點共線、三線共...
-
定比分點定理
定比分點定理是與PQ無交點的一條線段。
定義 證明 定比分點補充公式
