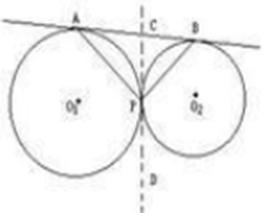
公切線性質
1.兩圓的兩條外公切線長相等；
2.兩條內公切線的長也相等。
3.兩圓的外公切線與連心線或者交於一點或者平行。
兩圓的外公切線如圖1所示。
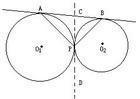圖1兩圓的外公切線數量關係
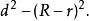公切線外公切線的長=根號下圓心距的平方-大圓半徑減小圓半徑的平方=
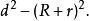公切線內公切線的長=根號下圓心距的平方-大圓半徑加小圓半徑的平方=
外公切線與連心線夾角的正弦值=圓心距分之大圓半徑減小圓半徑；
內公切線與連心線夾角的正弦值=圓心距分之大圓半徑加小圓半徑。
位置關係
公切線的條數與兩圓的位置關係如下：
若兩圓相離，則有4條公切線；
若兩圓外切，則有3條公切線（兩外切，一內切）；
兩圓相交，則有2條公切線（外切）；
若兩圓內切，則有1條公切線；
若兩圓內含，則有0條公切線。
尺規作圖方法
方法一：平移法（如圖2所示）
取圓O，圓O上的半徑OA，OB；
以B為圓心，以OA的長度為半徑畫圓交OB於C；
以為OO直徑畫圓D，以O為圓心，OC的長度為半徑畫圓，與圓D交與E；
連線OE並延長交圓O於F；
過O作OG||OF交圓G，則直線GF即為所求。
1.取圓O，圓O上的半徑OA，OB；
2.以B為圓心，以OA的長度為半徑畫圓交OB於C；
3.以為OO直徑畫圓D，以O為圓心，OC的長度為半徑畫圓，與圓D交與E；
4.連線OE並延長交圓O於F；
5.過O作OG||OF交圓G，則直線GF即為所求。
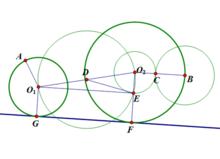圖2 平移法方法二：位似法（如圖3所示）
作圓O的一條半徑OA，在圓O中取一條與之平行的半徑OB；
連線BA，OO並延長交於P；
取PO中點C，以C為圓心，CP長為半徑畫弧交圓O於D，作直線PD，那么直線PD也與圓O圓O相切。
1.作圓O的一條半徑OA，在圓O中取一條與之平行的半徑OB；
2.連線BA，OO並延長交於P；
3.取PO中點C，以C為圓心，CP長為半徑畫弧交圓O於D，作直線PD，那么直線PD也與圓O圓O相切。
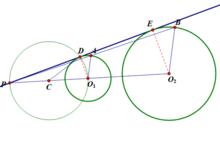圖3 位似法例題
作外公切線
已知：圓O半徑為R，O'半徑為r（假設R>r），求作它們的外公切線。
作法：
連線OO'，作出線段OO'的中點M；
以M為圓心，MO為半徑畫圓；
以O為圓心，R-r為半徑畫圓，與圓M的交點記作A、A'；
作射線OA交圓O於Q，過O'作OQ的平行線，交圓O'於P；
過P、Q作直線，直線PQ即為所求（如圖4所示） 。
1.連線OO'，作出線段OO'的中點M；
2.以M為圓心，MO為半徑畫圓；
3.以O為圓心，R-r為半徑畫圓，與圓M的交點記作A、A'；
4.作射線OA交圓O於Q，過O'作OQ的平行線，交圓O'於P；
5.過P、Q作直線，直線PQ即為所求（如圖4所示） 。
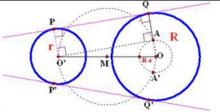圖4 作外公切線作內公切線
連OO'，作出線段OO'的中點M；
以M為圓心，MO為半徑畫圓
以O為圓心，R+r為半徑畫圓，與圓M的交點記作A，A'；
作射線OA交圓O於Q，過O'作OQ的平行線，交圓O'於P；
過P、Q作直線，直線PQ即為所求（如圖5所示）。
1.連OO'，作出線段OO'的中點M；
2.以M為圓心，MO為半徑畫圓
3.以O為圓心，R+r為半徑畫圓，與圓M的交點記作A，A'；
4.作射線OA交圓O於Q，過O'作OQ的平行線，交圓O'於P；
5.過P、Q作直線，直線PQ即為所求（如圖5所示）。
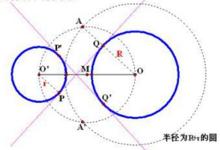圖5 內公切線