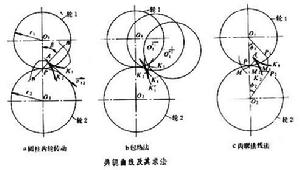
共軛曲線
正文
兩構件上用以實現給定運動規律的連續相切的一對曲線。曲線與尖點接觸可看作為共軛曲線的特例。齒輪傳動中一個齒輪推動另一個齒輪轉動和凸輪機構中凸輪推動從動件按要求的規律運動,都是依靠共軛曲線來完成的。單就齒輪傳動來說,通過做成齒廓的一對對共軛曲線可以得到滿足要求傳動比的轉動(如圓柱齒輪傳動),或進行轉動與移動間的運動轉換(如齒輪與齒條傳動),也可獲得變速運動(如非圓齒輪傳動)等。作為平面運動的一對共軛曲線與一對瞬心線(見瞬心)相同之處都是點接觸,但瞬心線之間是純滾動,而共軛曲線在接觸點處存在滑動。以共軛曲線作為構件廓線的共軛曲線機構,在傳遞運動的同時也一定存在有同樣運動規律的一對瞬心線。例如一對等速比傳動的圓柱齒輪,其瞬心線為相互滾動的一對節圓(見圖)。
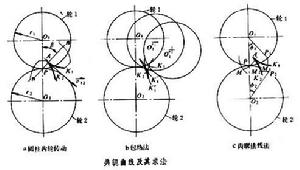 共軛曲線
共軛曲線給出兩構件的運動要求和共軛曲線中的一條曲線,就可求出另一條曲線,常用的有包絡法和齒廓法線法。
包絡法 根據一對共軛曲線在相對運動過程互為包絡線的原理,如果給定其中一條曲線K1及兩輪相對滾動的一對瞬心線(如圖中的兩節圓)使輪1對輪2作相對運動,即令輪2固定,節圓1在節圓 2上滾動,可得到K1在輪2上的一系列相對位置K1、K媷、K媹、…。這些曲線形成一個曲線族。作這個曲線族的包絡線K2,即使K2與曲線族中的每條曲線都相切,K2與K1即為一對共軛曲線。K2不僅可用圖解法求得,也可採用解析法。解析法首先是在輪1和輪2上分別加上兩個動標,在動標1上寫出曲線K1的方程f(x1,y1)=0,給出兩輪的轉角關係φ2=φ2(φ1),然後用坐標轉換的方法求得K1在動標2上的曲線族方程f(x2,y2,φ1)=0,則包絡線方程即為
f(x2,y2,φ1)=0 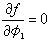
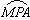 。
。 一對共軛曲線也可通過第三條曲線來獲得,如曲線3分別與曲線1和曲線2共軛,則1、2兩條曲線一定也能共軛。用齒條型刀具加工一對齒輪是其套用實例。
評價一對共軛曲線的優劣,除滿足運動要求外,還應考慮嚙合特性,如壓力角、滑動率、誘導曲率和有無干涉等。
一對共軛曲線的曲率計算可以套用歐拉-薩伐里公式:
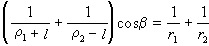
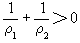 。
。 參考書目
Ф.Л.李特文著,盧賢占等譯:《齒輪嚙合原理》第二版,上海科學技術出版社,上海,1984。(Ф.Л.Литвин,Τеориязубчаmыхэацеплений, Изд. Науκа,Μосκва,1968.)