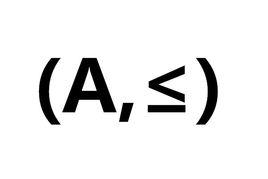定義
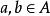 全序集
全序集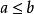 全序集
全序集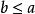 全序集
全序集 全序集
全序集設R為非空集合A上的偏序關係,如果任意的 ,都有 或 ,則稱R為A上的 全序關係(或 線序關係),且 構成一個 全序集或 鏈。
由定義可以知道,全序集的哈斯圖是一條直線段 。
 全序集
全序集 全序集
全序集 全序集
全序集任一偏序集,若任意且S中存在最小元,則稱為良序集。
 全序集
全序集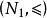 全序集
全序集 全序集
全序集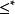 全序集
全序集若兩個全序集的元素相同,並且序關係也相同,則稱這兩個全序集是相同的,即當用列舉法表示全序集時,通常規定從左到右表示元素的順序。例如,設N為自然數集,關係“≤”為平常的數的小於或等於關係,則全序集表示為;若序關係“”定義為
 全序集
全序集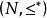 全序集
全序集 全序集
全序集則全序集表示為。
良序集與全序集
定理1
每一個良序集一定是全序集 。
注意:全序集不一定是良序集。
 全序集
全序集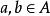 全序集
全序集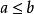 全序集
全序集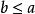 全序集
全序集 全序集
全序集證明: 設 是良序集,則對於任意的 構成的子集一定存在最小元,該最小元不是a就是b,因此一定滿足 或 ,所以 是全序集。
定理2
任一個有限的全序集一定是良序集。
 全序集
全序集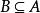 全序集
全序集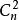 全序集
全序集 全序集
全序集證明:設 是任一有限全序集, 為任一非空子集,則B也是全序集。設B中有n個元素,將B中的元素依次進行比較,找出最小的那個元素,則最多進行 次比較,即 可找出最小元,因此是良序。
例題解析
 全序集
全序集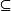 全序集
全序集 全序集
全序集例1 給定 上的包含關係 ,則 構成全序集。
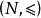 全序集
全序集例2 給定自然數集N上的小於等於(≤)關係,則 構成全序集。
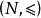 全序集
全序集例3 給定自然數集N上的小於等於(≤)關係,則 是良序集合。
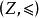 全序集
全序集例4 給定整數集Z上的小於等於(≤)關係,則 構成全序集。但因為在整數集上不存在最小元,所以該偏序集不是良序集。
常見全序集
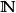 全序集
全序集 全序集
全序集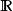 全序集
全序集1、 自然數集 、有理數集 、實數集 在通常的大小序下是全序的。
2、 有限長度的序列按字典序是全序的。最常見的是單詞在字典中是全序的。
3、 任何良序集是全序的。
 全序集
全序集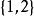 全序集
全序集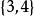 全序集
全序集4、 自然數的子集按集合包含關係是一個偏序,但不是全序的,即 不是全序的。因為 與 是不可比較的。