簡介
克利福德代數是外代數的推廣。設V是特徵不為2的域K上的向量空間，Q是V上的一個二次型，T(V)是V上的張量代數。若I是T(V)中下列形式的元素生成的理想：
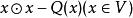克利福德代數則商代數C(V，Q)=T(V)/I稱為關於二次型Q的一個克利福德代數。當dim V=n時，dim C(V，Q)=2。當Q=0時，C(V，Q)即為V上的外代數。因此，克利福德代數是外代數的推廣。實數域上的複數全體，四元數全體都構成克利福德代數。
詳細定義
克利福德代數是由二次型定義的一類代數。它對研究二次型、正交群和多複變函數有重要作用。域F上有限維向量空間V上二次型Q，它是V到F的一個映射：x→Q(x)，x∈V，滿足：
1.Q(αx)=α²Q(x) (α∈F，x∈V).
2.B(x，y)=Q(x+y)-Q(x)-Q(y)，是雙線性的，也是對稱的.
若V為t個V的張量積：VV…V，V=F，則
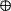克利福德代數
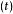克利福德代數T(V)= V
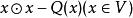克利福德代數是V的張量代數。由一切元 生成T(V)的一個理想K，其商代數：
C(V，Q)=T(V)/K
稱為二次型Q的克利福德代數。其元素為u-=u+K，u∈T(V)。由於T(V)是由V生成的，所以V到C(V，Q)的自然映射i：x→x-=x+K，x∈V，使得i(V)就生成C(V，Q).事實上，若：
dim V=n，
且u，u，…，u為V的基，則u-，u-，…u-(i<i<…<i， 1<r≤n)生成F上向量空間C(V，Q)。從而
dim C(V，Q)≤n².
特別地，若n=2且B(x，y)是非退化的，則C(V，Q)是四元數代數。克利福德代數具有泛性質：若f是V到一個代數A的線性映射，使得：
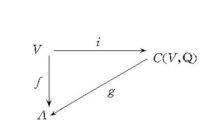克利福德代數f(x)²=Q(x)1， x∈V，
則存在C(V，Q)到A惟一的代數同態g使得如圖交換。
外代數
外代數亦稱格拉斯曼代數。各階反變張量空間的並構成的代數。用Λ(V)記形式和：
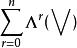克利福德代數
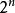克利福德代數則Λ(V)是維向量空間。設：
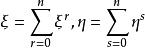克利福德代數
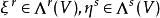克利福德代數其中。ξ與η的外積是：
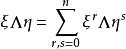克利福德代數則Λ(V)關於外積成為一個代數，稱為向量空間V的外代數或格拉斯曼代數。
向量空間Λ(V)的基底是{1，e，e∧e，…，e∧…∧e}(1≤i≤n，1≤i<i≤n).
同樣，人們也有對偶空間V*的外代數：
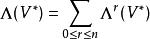克利福德代數
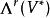克利福德代數的元素稱為向量空間上的r次外形式，它是V上反對稱r重線性函式。
人物簡介
英國數學家。生於埃克塞特(Exeter)，卒於馬德拉(M-adeira)1860年在倫敦國王學院就學，三年後入劍橋三一學院。1867年榮獲史密斯數學獎。第二年當選為該校套用數學教授。1874年成為皇家學會會員。克利福德在數學和物理學中的影響都很大。他將黎曼等人的非歐幾何引入英國，並在有關四次方程、軌跡分類、黎曼曲面的拓撲結構等方面有獨到見解，還創設了一種具有特殊性質的二階曲面來研究曲面的幾何結構，被稱為“克利福德曲面”。這些成果對克萊因等人的工作有所幫助，也為相對論的建立提供了理論依據。在代數方面，克利福德繼哈密頓的四元數之後，引入了新的超複數——八元數(biquaternion)，並推廣為更一般的“克利福德代數”。
發展
克利福德代數（ Clifford algebra）的主要貢獻者有：Hamilton（四元數），Grassmann（外代數），Clifford，Hestenes等等。
Hestenes是克利福德代數的發揚光大者，Hestenes的主要著作有：
《Space-time algebra》（ 克利福德代數被引入到狹義相對論中）。
《Clifford Algebra to Geometric Calculus》（ 克利福德代數結合了微積分，成為更強大的數學工具）
《New Foundations for Classical Mechanics》（經典物理學用 克利福德代數重新書寫）
還有一些將Clifford algebra套用於其他領域如廣義相對論、量子力學、量子場論、射影幾何、微分幾何、共形幾何等中的著作。
