代數
數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算,字元代表未知數或未定數。如果不包括除法 (用整數除除外),則每一個表達式都是一個含有理係數的多項式。例如: 1/2 xy+1/4z-3x+2/3. 一個代數方程式 (參見EQUATION)是通過使多項式等於零來表示對變數所加的條件。如果只有一個變數,那么滿足這一方程式的將是一定數量的實數或複數——它的根。一個代數數是某一方程式的根。代數數的理論——伽羅瓦理論是數學中最令人滿意的分支之一。建立這個理論的伽羅瓦(Evariste Galois,1811-32)在21歲時死於決鬥中。他證明了不可能有解五次方程的代數公式。用他的方法也證明了用直尺和圓規不能解決某些著名的幾何問題(立方加倍,三等分一個角)。多於一個變數的代數方程理論屬於代數幾何學,抽象代數學處理廣義的數學結構,它們與算術運算有類似之處。參見,如: 布爾代數(BOOLEAN ALGEBRA);群 (GRO-UPS);矩陣(MATRICES);四元數(QUA-TERNIONS );向量(VECTORS)。這些結構以公理 (見公理法 AXIOMATICMETHOD) 為特徵。特別重要的是結合律和交換律。代數方法使問題的求解簡化為符號表達式的操作,已滲入數學的各分支。
設K為一交換體. 把K上的向量空間E叫做K上的代數,或叫K-代數,如果賦以從E×E到E中的雙線性映射.換言之,賦以集合E由如下三個給定的法則所定義的代數結構:
——記為加法的合成法則(x,y)↦x+y;
——記為乘法的第二個合成法則(x,y)↦xy;
——記為乘法的從K×E到E中的映射(α,x)↦αx,這是一個作用法則;
這三個法則滿足下列條件:
a) 賦以第一個和第三個法則,E則為K上的一個向量空間;
b) 對E的元素的任意三元組(x,y,z),有
x(y+z)=xy+xz(y+z)x=yx+zx;
c)對K的任一元素偶(α,β)及對E的任一元素偶(x,y),有(αx)(βy)=(αβ) (xy).
設A為一非空集合. 賦予從A到K中的全體映射之集ℱ(A,K)以如下三個法則:
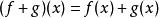 對稱代數
對稱代數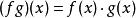 對稱代數
對稱代數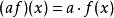 對稱代數
對稱代數則ℱ(A, K)是K上的代數, 自然地被稱為從A到K中的映射代數.當A=N時, 代數ℱ(A,K)叫做K的元素序列代數.
無論是在代數還是在分析中,代數結構都是最常見到的結構之一。十九世紀前半葉末,隨著哈密頓四元數理論的建立,非交換代數的研究已經開始. 在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了. 到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展.
與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了起來.
對稱代數
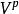 對稱代數
對稱代數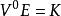 對稱代數
對稱代數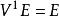 對稱代數
對稱代數對稱代數是概括多元多項式代數的一種代數。設E是特徵為0的域K上的向量空間, 是E的p次對稱冪,約定 , ,記:
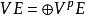 對稱代數
對稱代數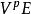 對稱代數
對稱代數是 的直和,∨E對乘法:
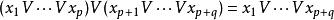 對稱代數
對稱代數構成一個K上的交換的結合代數,稱為E上的對稱代數。1是∨E的單位元且∨E由{E,1}生成.設u∈∨E,若:
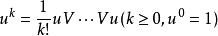 對稱代數
對稱代數則:
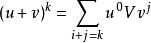 對稱代數
對稱代數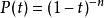 對稱代數
對稱代數對任意u,v∈∨E。E上的對稱代數在同構的意義下是惟一的。若dim E=n,則∨E的龐加萊級數。K上的n元多項式的代數K[x,x,…,x]就是一種對稱代數。
結合代數
類似於環、域,而更接近於環的一個代數系.設A是一個結合環,若A又是域F上向量空間,且對任意元素a,b∈A,λ∈F,適合λ(ab)=(λa)b=a(λb),則稱A是F上結合代數,簡稱F代數.稱F上向量空間A的維數為代數A的維數,記為dimA.一般地,若結合環A又是左R模,其中R是有單位元1的交換環,且對任意a∈A,λ∈R,適合
1·a=a,λ(ab)=(λa)b=a(λb),
則稱A是R上代數.通常假定一個R代數有單位元.
結合代數研究的中心問題是刻畫各類代數的結構,它是從19世紀50年代哈密頓(Hamilton,W.R.)引入實域上四元數(1843年)、格拉斯曼(Grassmann,H.G.)引入向量乘法以及凱萊(Cayley,A.)等人討論矩陣代數開始的.到20世紀初,韋德伯恩(Wedderburn,J.H.M.)開創了有限維代數發展的新階段,他的半單代數結構理論對代數的發展起了推動作用,使有限維代數的研究基本上歸結為冪零代數與可除代數的研究,進而得出半單代數較完整的表示理論.阿爾貝特(Albert,A.A.)的《代數結構》一書(1939年)是對經典代數的很好的總結.非半單代數結構的研究則較為複雜,因此劃分成一些自然的代數類並對它們進行描述就成了占主要地位的工作.克德(Ko¨the,G.)、中山正(Nakayama,T.)、淺野啟三(Asano,K.)等人刻畫了主理想代數、弗羅貝尼烏斯代數以及它們的推廣.近年來,開始用模論的方法研究代數結構,產生了代數表示論(參見“代數表示論”).
由於R上代數A與環的概念僅多一個R×A到A的乘法運算,因此,子代數、單側理想、理想、商代數、冪零和冪零理想、同構及同態等概念僅比環中相應概念多一個與R中元相乘封閉的性質,不再重複它們的定義.
左對稱代數
左對稱代數(或Vinberg代數,Koszul代數,擬結合代數等)是一類重要的非結合代數。它在數學和數學物理中起重要作用。它的研究可以直接促進其它相關領域的研究,如李群,李代數,非交換幾何,量子場,可積系統,微分幾何等。左對稱代數在各個領域的廣泛套用吸引了許多學者的注意,比如數學大師如以及菲爾茲獎獲得者Zelmanov Connes,Novikov等。
左對稱代數出現的比較早,最早是在1896年Cayley研究根樹代數時提出的,但直到1960年才重新引起人們的注意,此時Vinberg套用左對稱代數分類凸齊次錐,Milnor和Auslander將仿射平坦流形與左對稱代數聯繫起來。之後就陸陸續續的出現了與左對稱代數相關的很多不同領域的文章,左對稱代數得到了越來越多的人的重視,也取得了一些成果。比如說Kreimer和Kontsevich將左對稱代數與數學物理中的量子場理論以及重正化理論聯繫起來,還有和Bakalov和Kac在頂點代數的研究中也套用到有關左對稱代數的理論。
設G是一個連通的,單連通的李群,在G的切叢T(G)=g中按通常的括積,則g成為李代數,這就是李群的李代數。除此之外,聯絡還與李代數中的另一個運算有關,由其我們引出左對稱代數的概念。
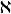 對稱代數
對稱代數M是一個流形, 為其上所有的可微向量場的李代數。
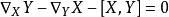 對稱代數
對稱代數仿射聯絡是無扭的,如果:
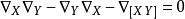 對稱代數
對稱代數仿射聯絡是平坦的,如果:
這樣一個平坦的無扭的仿射聯絡確定了下面的共變微分:
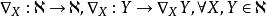 對稱代數
對稱代數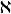 對稱代數
對稱代數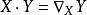 對稱代數
對稱代數如果我們在 定義 ,則(1)(2)分別等價於下列等式:
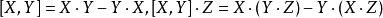 對稱代數
對稱代數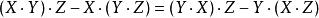 對稱代數
對稱代數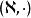 對稱代數
對稱代數運算·滿足 ,稱滿足這種條件的代數為左對稱代數,從而 是一個左對稱代數。
