定義
為了便於進行空間坐標的變換，需要建立起描述像點在像空間位置的坐標系，即像空間坐標系（S-xyz），該坐標系是一種過渡坐標系，用來表示像點在像方空間的位置。
性質
像空間坐標系以攝站點（或投影中心）S為坐標原點，攝影機的主光軸So為坐標系的z軸，像空間坐標系的x、y軸分別與像平面坐標系的x、y軸平行。該坐標系可以很方便地與像平面坐標系聯繫起來。在這個坐標系中，每一個像點的z坐標都等於So的長，但符號是負的。
套用
像空間坐標系（1）確定影像內方位元素的基準坐標系
影像的內方位元素是指確定攝影機的鏡頭中心（嚴格地說，應該是鏡頭的像方節點）相對於影像位置關係的參數。內方位元素包括以下3個參數：像主點（主光軸在影像面上的垂足）相對於影像中心的位置x、y以及鏡頭中心到影像面上的垂距f（也稱主距），如圖所示。對於航空影像，x、y即像主點在框標坐標系中的坐標。
（2）空間直角坐標系的旋轉變換
像點空間直角坐標的旋轉變換是指像空間坐標與像空間輔助坐標之間的變換。由高等數學可知，空間直角坐標的變換是正交變換，一個坐標系按某種順序依次地旋轉三個角度即可變換為另一個同原點的坐標系。
設像點a在像空間坐標系中的坐標為（x，y，-f），而在像空間輔助坐標系中的坐標為（X，Y，Z），兩者之間的正交變換關係可以用下式表示：
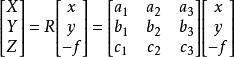像空間坐標系或
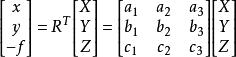像空間坐標系式中R為一個3×3階的正交矩陣，它由9個方向餘弦所組成。
（3）共線條件方程的基準坐標系之一
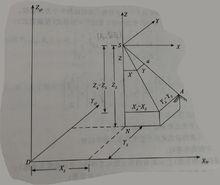
像空間坐標系共線方程是中心投影構像的數學基礎，也是各種攝影測量處理方法的重要理論基礎，例如單像空間後方交會、雙像空間前方交會以及光束法區域網平差等一系列問題的原理，都是以共線條件作為出發點的，只是隨著所處理問題的具體情況不同，共線條件的表示形式和使用方法也有所不同。
如圖所示，S為攝影中心，在某一規定的物方空間坐標系中其坐標為（X，Y，Z），A為任一物方空間點，它的物方空間坐標為（X，Y，Z）。a為A在影像上的構像，相應的像空間坐標和像空間輔助坐標分別為（x，y，-f）和（X，Y，Z）。攝影時S、A、a三點位於一條直線上，那么像點的像空間輔助坐標與物方點物方空間坐標之間有以下關係：
像空間坐標系則
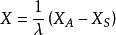像空間坐標系
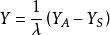像空間坐標系
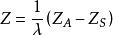像空間坐標系利用（2）中像空間坐標與像空間輔助坐標的關係，將上式展開為
像空間坐標系
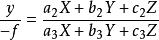像空間坐標系考慮到像主點的坐標x，y，得
像空間坐標系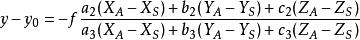
像空間坐標系這就是常見的共線條件方程式（簡稱共線方程）。
式中：x，y為像點的像平面坐標；
x，y為影像的內方位元素
X，Y，Z為攝站點的物方空間坐標；
X，Y，Z為物方點的物方空間坐標；
a，b，c（i=1，2，3）為影像的3個外方位角元素組成的9個方向餘弦。
