定義
流函式是流體力學中同連續性方程相聯繫的一個標量函式，它在流體平面運動和軸對稱運動中有重要套用。不可壓縮流體和定常可壓縮流體的連續性方程可寫成(1)式 。式中 v 為速度矢量；ρ為流體密度；ν=0和ν=1分別對應於不可壓縮流體和定常可壓縮流體情形。由方程（1）容易看到存在著矢勢B，使（2）成立：
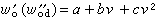流函式式中B稱為廣義流函式。在平面運動和軸對稱運動這兩種特殊情形下，B只有一個非零分量，如果引進流函式將來以一個函式代替兩個速度分量函式的好處。在平面運動情形下連續性方程在直角坐標系中可以寫成如下的形式：
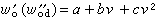流函式式中u、v為速度矢量在x、y軸方向上的分量。由此推出存在流函式Ψ，使得：
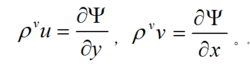流函式顯然，此時有B=（0，0，Ψ），Ψ稱為平面運動的流函式。在軸對稱運動中，取柱坐標系（r，φ，z）和球坐標系（r，φ，θ），連續性方程可分別寫為：
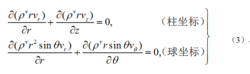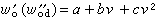流函式流函式式中v、v和v、v分別為速度矢量在柱坐標r、z軸上和球坐標系r、θ軸上的分量。由式（3）推出存在著流函式Ψ，使得：
容易驗證，此時矢勢具有下列形式：
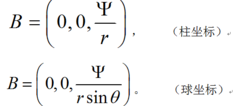流函式性質
Ψ稱為軸對稱運動的流函式，也稱為斯托克斯流函式。對於不可壓縮流體，流函式具有下列四個性質：
①Ψ可加上任一常數而不影響對流體的運動的描述。
②Ψ為常數的曲面是流面。
③在Oxy平面上或θ=π/2的平面上取一曲線弧AB，則通過以AB為底、高為單位的曲面（平面情形）或通過以AB為母線的鏇轉曲面（軸對稱情形）的流量Q與流函式在A、B兩點上的值Ψ和Ψ之間存在如下關係：
Q=（2π）（Ψ－Ψ），
式中v=0和v=1分別對應於平面和軸對稱情形。
④在單聯通區域內若不存在源、匯（見源流、匯流），則流函式Ψ是單值函式。若單聯通區域內有源，匯或在多聯通區域內，則Ψ一般是多值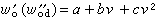函式。
流函式如果不可壓縮流體的運動是無鏇的，則▽×v=0。在直角坐標系中無鏇條件給出
,由此推出，流函式Ψ滿足拉普拉斯方程△Ψ=0，因而是調和函式。在柱坐標系和球坐標系中，無鏇條件要求：
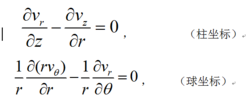流函式於是Ψ滿足下列方程：DΨ=0，式中D為廣義斯托克斯算符，它在柱坐標系和球坐標系中的表達式分別為：
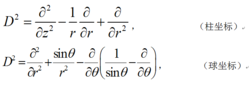流函式總結
1、對於不可壓縮流的二維流動，無論是有鏇流動還是無鏇流動，流體有粘性還是沒有粘性，一定存在流函式。在三維流動中一般不存在流函式（軸對稱流動除外）。
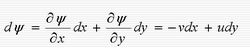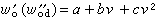流函式流函式2、對於不可壓縮流體的平面流動，流函式永遠滿足連續性方程。
3 流函式都有各自的常數值，流函式的等值線就是流線。
4、對於不可壓縮流體的平面勢流，流函式滿足拉普拉斯方程，流函式也是調和函式。
5、平面流動中，通過兩條流線間任意一曲線（單位厚度）的體積流量等於兩條流線的流函式之差，與流線形狀無關。
