解析攝影測量
正文
利用攝影機或其他感測器獲得的信息，使用解析方法進行測點、測圖或空中三角測量的技術。20世紀30年代以來，攝影測量基本上都是使用模擬式的解法。50年代以後，隨著數學計算機和計算技術的發展，攝影測量逐步由模擬方式向解析的方式過渡。最初是解析空中三角測量，60年代以後又出現了解析測圖儀和數字地形模型等。
基礎 像點在不同的空間坐標系中的坐標變換和用數學方式表達投影光線（像點、投影中心和地物點三點共線）與同名光線相交（兩同名光線共面），以建立立體模型，以及模型的絕對定向（模型點坐標的空間相似變換）等，這些都是解析攝影測量的最基礎的理論知識。
像點坐標變換式 設某像點的像空間坐標為x、у、-f，它的輔助空間坐標為X、Y、Z，投影中心S為這兩個坐標系的原點，則其坐標變換關係式(以矩陣形式表示)為：
，
，
，
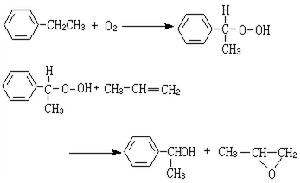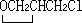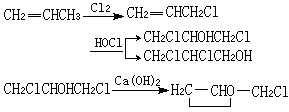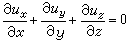
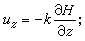
、X1、Y1、Z1為像點ɑ1在以S1為原點的輔助坐標系中的坐標值；X2、Y2、Z2為像點ɑ2在以S2為原點的輔助坐標系中的坐標值，這兩個坐標系相應的軸互相平行。 模型的絕對定向關係式 模型點空間坐標相似變換的關係式。它有坐標原點平移（3個參數）,模型的空間鏇轉（3個參數）和比例尺係數等7個待定參數。三維的線性相似變換式為：
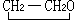
共線條件方程、共麵條件議程和空間相似變換關係式可分別用來解求像片的外方位元素、像對的相對方位元素和絕對方位元素，此時，需要將上述嚴密關係式線性化，在有多餘觀測條件下，用最小二乘法進行解算。
解析測圖儀 由立體坐標量測儀、電子計算機和電子繪圖桌以在線上方式組成的一種立體測圖系統。坐標儀的手輪和腳輪的鏇轉，通過編碼器將機械的移動量轉變為電脈衝信號，經過模／數轉換，將物空坐標輸入計算機或專用機(稱為數字投影器)，“實時”地作像點坐標的像差改正、解算共線方程等。計算得應有的像點坐標x、у,並由計算機反饋到立體坐標量測儀中,通過數／模轉換，控制伺服電機使像片盤或光學系統作理論上應該加入的額外移動。“實時”就是從數據輸入，作各種運算以及反饋到閉路系統的伺服電機作像盤的額外移動等，整個過程都應該在小於1/30秒的時間內完成，這樣，人在觀測中就不會感覺到有任何的跳動。當需要在線上繪圖時，電子計算機還可實時地控制繪圖桌，以圖解方式繪圖（圖3）。 有少數解析測圖儀是將像方坐標輸入計算機，這時，計算機要“實時”地計算並控制像片車架(或光學系統)的附加移動，以及計算相應模型點的物方空間坐標，控制繪圖桌進行繪圖。
解析測圖儀的測圖原理同常規的模擬型立體測圖儀的測圖原理基本相同，只是後者利用實際的投影光線或者用一對空間導桿代替空間光線，而解析測圖儀則利用一台專用的電子計算機實時地解算構像方程式來完成這項任務。測圖中的相對定向和絕對定向等操作過程，對兩類儀器來說也是基本相同的，但解析測圖儀完全是用計算機軟體來保證，故有較大的靈活性，幾乎能夠處理所有方式的攝影資料。由於立體模型是用解析方法形成的，可以改除各種像差的影響和減少儀器誤差，所以能夠得到較高的精度。
發展 計算機功能的不斷增強、價格不斷下降和解析方式的靈活性，促使解析攝影測量迅速發展。解析空中三角測量已得到普遍的套用，數字地形模型技術和解析測圖儀將逐漸地普及。解析攝影測量的原理將在地形和非地形攝影測量以及遙感圖像的幾何改正等各個領域中廣泛套用，並為攝影測量的自動化打下了基礎。解析攝影測量都是以數字運算為基礎的，在其發展中，有時為了強調數字的特點，對某些工種，習慣上又稱之為數字攝影測量。（見彩圖）。
