久期

久期也稱持續期，是1938年由F.R.Macaulay提出的。它是以未來時間發生的現金流，按照目前的收益率折現成現值，再用每筆現值乘以現在距離該筆現金流發生時間點的時間年限，然後進行求和，以這個總和除以債券目前的價格得到的數值就是久期。概括來說，就是債券各期現金流支付所需時間的加權平均值。

基本信息

• 中文名：久期
• 英文名：Duration

• 類別：定律
• 屬性：數學

數學解釋

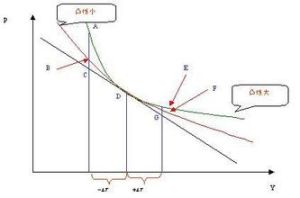久期

久期，全稱麥考利久期－Macaulay duration， 數學定義：如果市場利率是Y，現金流（X1,X2,...,Xn）的麥考利久期定義為：D(Y)=[1*X1/(1+Y)^1+2*X2/(1+Y)^2+...+n*Xn/(1+Y)^n]/[X0+x1/(1+Y)^1+X2/(1+Y)^2+...+Xn/(1+Y)^n]
即 D=(1*PVx1+...n*PVxn)/PVx
其中，PVXi表示第i期現金流的現值，D表示久期。
通過下面例子可以更好理解久期的定義。
例子：假設有一債券，在未來n年的現金流為（X1,X2,...Xn），其中Xi表示第i期的現金流。假設利率為Y0，投資者持有現金流不久，利率立即發生升高，變為Y，問：應該持有多長時間，才能使得其到期的價值不低於利率為Y0的價值？
通過下面定理可以快速解答上面問題。
定理：PV(Y0)*(1+Y0)^q