偏微分方程初值問題差分方法
正文
一種求解偏微分方程初值問題的主要數值方法。許多連續介質的運動過程都可表示成含時間 t的偏微分方程。最簡單的有雙曲型的對流方程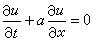 (1)
(1)
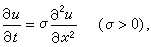 (2)
(2)
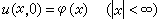 (3)
(3)
初值問題(1)、(3)的解為
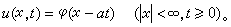 (4)
(4)
微分方程定解問題的離散化(差分格式的建立) 以初值問題(1)、(2)為例,在x-t平面上作兩族平行於坐標軸的直線
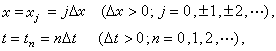
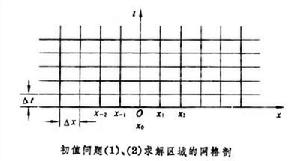 所示(格線線之間的距離,也可以是不相等的)。格線線的交點叫作格點,在格點(jΔx,nΔt)上,由數值微分公式
所示(格線線之間的距離,也可以是不相等的)。格線線的交點叫作格點,在格點(jΔx,nΔt)上,由數值微分公式 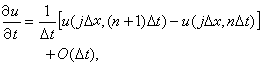
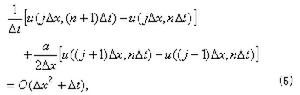
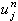 表示這差分方程的解,則
表示這差分方程的解,則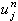 適合
適合 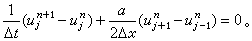 (6)
(6)
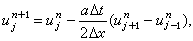 (7)
(7)
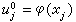 算出
算出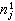 ,
,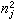 ,…等。
,…等。 離散化過程並不惟一,因而可有不同的差分格式。例如,由
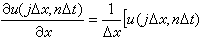
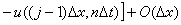 (8)
(8)
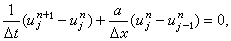 (9)
(9)
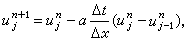
差分格式的相容性 當Δt和Δx都趨於零時,若差分格式的截斷誤差也趨於零,則稱差分格式與微分方程是相容的。相容性說明Δt和Δx越小差分方程與微分方程越接近。上面的差分方程 (7)和(9)都是微分方程(1)的相容格式。
差分格式的收斂性 設P(
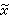 ,
,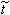 )是求解區域中的一點,取Δx與Δt使
)是求解區域中的一點,取Δx與Δt使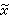 =jΔx,
=jΔx,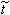 =nΔt用差分格式算出
=nΔt用差分格式算出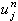 。如果當Δt和Δx趨於零時,
。如果當Δt和Δx趨於零時,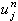 -u(
-u(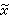 ,
,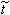 )也趨於零,則可用
)也趨於零,則可用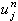 作微分方程的解u(jΔx,nΔt)的近似,並稱此差分格式是收斂的。
作微分方程的解u(jΔx,nΔt)的近似,並稱此差分格式是收斂的。 庫朗條件 也稱CFL條件,是A.A.庫朗、K.O.弗里德里希斯和H.盧伊三人1928年在一篇著名文章中提出的。雙曲線微分方程的解, 對某一點(
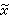 ,
, 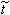 )而言,在初值區域內有一個依賴區域。差分方程也是如此。對同一個微分方程,相容但不相同的差分格式的依賴區域可以不同。對於差分格式(7),點(jΔx,nΔt)的依賴區域是初值線,t=0上的區間【(j-n)Δx,(j+n)Δx】。如令Δt/Δx=r=常數,
)而言,在初值區域內有一個依賴區域。差分方程也是如此。對同一個微分方程,相容但不相同的差分格式的依賴區域可以不同。對於差分格式(7),點(jΔx,nΔt)的依賴區域是初值線,t=0上的區間【(j-n)Δx,(j+n)Δx】。如令Δt/Δx=r=常數,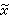 =jΔx,
=jΔx,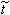 =nΔt,則點
=nΔt,則點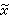 、
、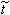 的依賴區域為【
的依賴區域為【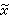 -
-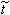 /r,
/r,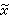 +
+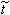 /r】,可見對於固定點(
/r】,可見對於固定點(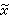 ,
,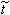 ),若步長比r固定,依賴區域的大小與Δt和Δx 的大小無關。差分方程(9)的依賴區域則是【
),若步長比r固定,依賴區域的大小與Δt和Δx 的大小無關。差分方程(9)的依賴區域則是【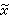 -t/r,
-t/r,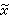 】。庫朗條件是:差分格式收斂的一個必要條件是差分方程的依賴區域包含微分方程的依賴區域。用它可判斷哪些格式不收斂。 微分方程(1)在點(
】。庫朗條件是:差分格式收斂的一個必要條件是差分方程的依賴區域包含微分方程的依賴區域。用它可判斷哪些格式不收斂。 微分方程(1)在點(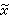 ,
,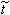 )處的依賴區域是點(
)處的依賴區域是點(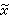 -α
-α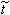 ,0)。所以,格式(7)的庫朗條件是
,0)。所以,格式(7)的庫朗條件是 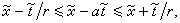
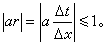 格式(9)的庫朗條件則是
格式(9)的庫朗條件則是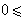
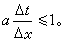 同時,庫朗條件指出α<0時,格式(9)不收斂。因此當α<0時,格式(9)是無用的。
同時,庫朗條件指出α<0時,格式(9)不收斂。因此當α<0時,格式(9)是無用的。 庫朗條件只是收斂的必要條件。收斂性還需有正面證明,當α>0時,格式(9)在庫朗條件
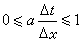 (10)
(10)
如果α<0,當
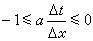 時,格式
時,格式 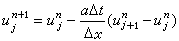
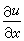 用向後差商往上風取近似值;當α<0時,用向前差商代替
用向後差商往上風取近似值;當α<0時,用向前差商代替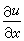 ,同樣也是往上風取近似值。
,同樣也是往上風取近似值。 差分格式的穩定性 用一個差分格式計算
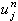 時,初值
時,初值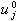 的誤差必然要影響到後面的
的誤差必然要影響到後面的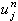 ,但希望這誤差的影響不要越來越大以致完全歪曲了差分方程的真解,這便是穩定性問題。對於常係數線性偏微分方程的穩定性理論,J.馮·諾伊曼系統地運用傅立葉分析作了研究,把差分方程的解表示成諧波的疊加,考察其中一個諧波
,但希望這誤差的影響不要越來越大以致完全歪曲了差分方程的真解,這便是穩定性問題。對於常係數線性偏微分方程的穩定性理論,J.馮·諾伊曼系統地運用傅立葉分析作了研究,把差分方程的解表示成諧波的疊加,考察其中一個諧波 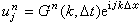 (11)
(11)
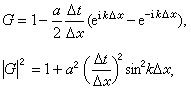
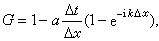
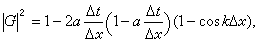
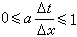 ,即滿足庫朗條件時,|G|≤1,所以格式(9)是穩定的。
,即滿足庫朗條件時,|G|≤1,所以格式(9)是穩定的。 對於擴散方程的初值問題(2)、(3),採用記號
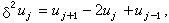
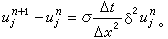 (12)
(12)
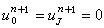 (13)
(13)
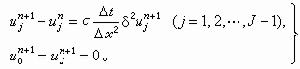 (14)
(14)
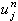 直接計算
直接計算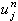 +1,叫做顯式格式。顯式格式與(2)是相容的,它的截斷誤差為 O(Δx2+Δt);如
+1,叫做顯式格式。顯式格式與(2)是相容的,它的截斷誤差為 O(Δx2+Δt);如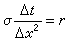 為常數, 則當
為常數, 則當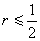 時它是收斂的和穩定的,帶有邊值條件的差分格式(14),是含未知數
時它是收斂的和穩定的,帶有邊值條件的差分格式(14),是含未知數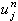 +1(j=1,2,…,J-1)的一組線性聯立方程組, 這種格式叫做隱式格式。它的解存在、惟一,並且可用追趕法求解。當r取任何正值時,它都是穩定的,其截斷誤差也是O(Δx2+Δt),由於r無限制,Δt比顯式格式可相對取得大一些,當然Δt太大了,也要影響到截斷誤差。
+1(j=1,2,…,J-1)的一組線性聯立方程組, 這種格式叫做隱式格式。它的解存在、惟一,並且可用追趕法求解。當r取任何正值時,它都是穩定的,其截斷誤差也是O(Δx2+Δt),由於r無限制,Δt比顯式格式可相對取得大一些,當然Δt太大了,也要影響到截斷誤差。 把格式(12)和(14)組合起來,又可有格式
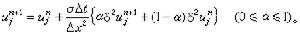
(15)
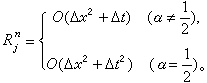
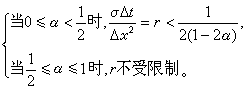
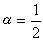 時,這格式叫荷瑞克-尼考松格式,
時,這格式叫荷瑞克-尼考松格式, 它也是隱式格式,它的截斷誤差是O(Δx2+Δt2)比四點隱式格式(14)好,但工作量卻略大一些。
它也是隱式格式,它的截斷誤差是O(Δx2+Δt2)比四點隱式格式(14)好,但工作量卻略大一些。 拉克斯等價定理 對於線性偏微分方程組的適定的初值問題,一個與之相容的線性差分格式收斂的充分必要條件是這格式是穩定的。
這個重要定理說明,在差分格式的收斂性與穩定性兩個問題中,對於適定的線性偏微分方程問題,只須證明比較容易證明的相容性與穩定性。
參考書目
R.D.Richtmyer and K.M.Morton,Difference Methods for Initial value Problems,2nd ed., Interscience, New York, 1967.
