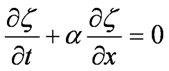對流方程

不為常數時，方程為一維變係數對流方程。 一維常係數對流方程的步長定律： 一維常係數對流方程的固有差分格式：

簡介

對流方程是最簡單的雙曲線偏微分方程。

一維對流方程

一維對流方程的形式如下所示：
其中，ζ 代表物質的量，α 代表物質的運動速度。此一維對流方程僅僅表示物質的運動情況，而與邊界條件或是約束條件無關。當 α 為常數時，此一維對流方程為一維常係數對流方程，當 α 不為常數時，方程為一維變係數對流方程。在不考慮邊界條件或約束條件的情況下，無論 α 是否為常數，此對流方程本身的數值解法存在固有的有限差分格式，條件是要滿足步長定律。
一維常係數對流方程的步長定律：
α · △t╱△x = 1 , 其中 △t 為時間步長，△x 為空間步長。
一維常係數對流方程的固有差分格式：
或者
若將變係數α在每步長內看作為常數，那么以上結論也適合解變係數對流方程。