保形溶液理論
正文
建立在對應態原理基礎上的一種溶液理論。如果一對分子的勢能ε是分子間距r的函式,且僅包含兩個特徵參數ε*和r*,則ε=ε*φ(r/r*)
式中r*是兩個分子處於其勢能最低點處的距離;ε*是位於此距離時勢能的數值。凡具有相同的勢能函式φ,只是一對分子的相互作用特徵參數ε*和r*有所差別的一組液體,稱為保形液體。設有某一保形液體,其分子參數ε*和r*與另一選定的參考保形液體的分子參數ε奵和r奵只有很小差別,被看成對參考液體的微擾,令f=ε*/ε奵,1/g=r*/r奵。設總勢能等於全部成對分子相互作用能之和。在f 和g 接近於1時,將自由能F圍繞著參考物質的 ε奵和r奵展開成泰勒級數,只取與(ε*-ε奵)和(r*-r奵)成正比的項(稱為一級微擾),推導得溶液的吉布斯函式為:
G=G0+U0(f-1)+3(NkT-pV0)(g-1)
式中G0、U0、V0為參考物質的吉布斯函式、內能和體積;N為分子數;k為玻耳茲曼常數;T為熱力學溫度;p為壓力。上式以參考物質的熱力學性質和分子參數來表達某種液體的熱力學性質,是對應態原理的一種表達形式。將此原理套用於溶液,認為在該混合物與構成它的純組分均符合此原理的條件下,把溶液等價於一種受到微擾的假想液體,使用了完全無規的條件,推導出: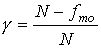
GE=x1x2U0(2f12-f11-f22)
保形溶液理論避免了使用具體的物理模型,因而可以用於檢驗其他具有物理模型的溶液理論。它的適用範圍嚴格限制於符合對應態原理的球形分子或接近於球形分子所構成的偏離理想溶液程度很小的混合物,能完全滿足其所要求的條件的溶液體系為數很少。