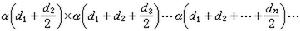似晶格理論
正文
由處理固體溶液發展而來的一種溶液理論,是描述大小相近的球形分子所構成的溶液的理論。X射線分析表明,液體和晶體有相似之處,考慮到液體中的短程有序性,把對固溶體的處理方法推廣到液體混合物,就成為似晶格溶液理論。假設溶液中存在似晶格結構,圍繞每個分子最鄰近的其他分子有一平均數目,叫做配位數,以z表示。假設兩種分子具有相似的大小和形狀,每個分子占據一個晶格,晶格是堅硬的,不因組成變化而變化,即混合過程體積不變,VE=0。假設混合物的位能可分解為兩項:①處在晶格的平衡位置處的分子的相互作用能;②各分子在平衡位置附近的振動能。混合物的配分函式Z為:
Z=Zc·Zv
式中處在晶格平衡位置的分子的配分函式為Zc,它隨混合物的組成而變;Zv為振動分子的配分函式。通過計算Zc就可以計算混合吉布斯函式。NA個A分子與NB個B分子混合,如果只考慮最鄰近分子的相互作用,則系統的位能就由所有最鄰近的分子貢獻而成,其混合吉布斯函式為: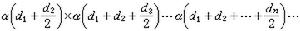
對上式求和,稱為布喇格-威廉斯近似,它考慮混合是完全無規的,上式中gi的總和有一最大項,其值為(NA+NB)!/(NA!NB!),以此代替gi的總和,並以完全無規情況下的NAB的平均值NAB=zNANB/(NA+NB)代入,可得過量吉布斯函式GE:
GE=xAxBN0zW
式中N0為阿伏伽德羅數;xA和xB為A和B的摩爾分數。過量熵為:SE=0
當W<0時,A、B分子有結合的傾向;當W >0時,有分離為兩個共存液相的傾向。實驗結果表明,過量熵可能為正值或負值,此理論不能解釋。如果溶液的交換能不是零,則會造成溶液中分子分布的不同程度的有序。另一種近似由E.A.古根海姆提出,稱為擬化學近似,它考慮混合過程類似於以下交換“反應”平衡: