前提
由於有效估計的基礎上的一種估計方法,所以在介紹有效估計之前,最小方差無偏估計的概念知識需要向大家提前介紹。
無偏估計是用樣本統計量來估計總體參數時的一種無偏推斷。估計量的數學期望等於被估計參數的真實值,則稱此此估計量為被估計參數的無偏估計,即具有無偏性,是一種用於評價估計量優良性的準則。無偏估計的意義是:在多次重複下,它們的平均數接近所估計的參數真值。無偏估計常被套用於測驗分數統計中 。
而具有最小方差的無偏估計的判別方法如下:
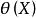 有效估計值
有效估計值 有效估計值
有效估計值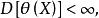 有效估計值
有效估計值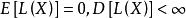 有效估計值
有效估計值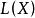 有效估計值
有效估計值設 是 的一個無偏估計, 若對任何滿足條件: 的統計量 ,有
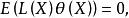 有效估計值
有效估計值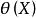 有效估計值
有效估計值 有效估計值
有效估計值則無偏估計 是 的最小方差無偏估計。
定義
由樣本值求得的估計值,方差越小,估計值接近待估參數的機率越大,種特性稱為估計的有效性 。
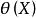 有效估計值
有效估計值 有效估計值
有效估計值設 是 的一個無偏估計,若
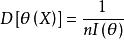 有效估計值
有效估計值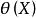 有效估計值
有效估計值 有效估計值
有效估計值則 是 的有效估計。
因為多次測定的平均值比單次測定值具有更好的精密度,因此,用平均值要比單次測定值xi作為總體均值μ的估計值更有效。在常態分配中,不知總體分布時,均值仍然可以作為分布的無偏估計值,但不是有效的。有結果(Gauss-Markov Theorem)指向這個結論,均值比總體均值μ的其他線性無偏估計值擁有更小的方差。
性質
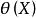 有效估計值
有效估計值 有效估計值
有效估計值(1)設是的任一無偏估計,稱
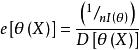 有效估計值
有效估計值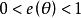 有效估計值
有效估計值為估計量的效率,且顯然。
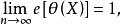 有效估計值
有效估計值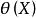 有效估計值
有效估計值(2)如果無偏估計量的效率滿足則稱為漸進有效估計。
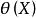 有效估計值
有效估計值(3)如果為有效估計,則它也是最小方差無偏估計,但反之卻不成立。

