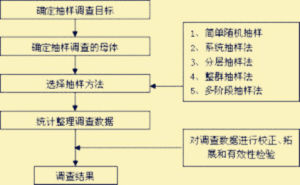
概念
PPS抽樣是以貨幣單位作為抽樣單元進行選樣的一種方法,有時也被稱為金額加權抽樣貨幣單位抽樣,累計貨幣金額抽樣,以及綜合屬性變數抽樣等。在該方法下總體中的每個貨幣單位被選中的機會相同,所以總體中某一項目被選中的機率等於該項目的金額與總體金額的比率。項目金額越大,被選中的機率就越大。但實際上註冊會計師並不是對總體中的貨幣單位實施檢查,而是對包含被選取貨幣單位的餘額或交易實施檢查。註冊會計師檢查的餘額或交易被稱為邏輯單元或實物單元。優點
PPS抽樣的優點包括下列方面:
(1)PPS抽樣一般比傳統變數抽樣更易於使用。由於PPS抽樣以礎,註冊會計師可以很方便地計算樣本規模,並手工或使用量表評價樣本結果。樣本的選取可以在電腦程式或計算器的協助下進行。
(2)PPS抽樣的樣本規模不需考慮被審計金額的預計變異性。傳統變數抽樣的樣本規模是在總體項目共有特徵的變異性或標準差的基礎上計算的。PPS抽樣在確定所需的樣本規模時不需要直接考慮貨幣金額的標準差。
(3)PPS抽樣中項目被選取的機率與其貨幣金額大小成比例,因而生成的樣本自動分層。如果使用傳統變數抽樣,註冊會計師通常需要對總體進行分層,以減小樣本規模。
(4)PPS抽樣中如果項目金額超過選樣問距,PPS系統選樣自動識別所有單個重大項目。
(5)如果註冊會計師預計沒有錯報,PPS抽樣的樣本規模通常比傳統變數抽樣方法更小
(6)PPS抽樣的樣本更容易設計,且可在能夠獲得完整的總體之前開始選取樣本。
缺點
PPS抽樣的缺點包括下列方面:
(1)使用PPS抽樣時通常假設抽樣單元的審定金額不應小於零或大於賬面金額。如果註冊會計師預計存在低估或審定金額小於零的情況,在設計PPS抽樣方法時就需要特別考慮。
(2)如果註冊會計師在PPS抽樣的樣本中發現低估,在評價樣本時需要特別考慮。
(3)對零餘額或負餘額的選取需要在設計時特別考慮。例如,如果準備對應收賬款進行抽樣,註冊會計師可能需要將貸方餘額分離出去,作為一個單獨的總體。如果檢查零餘額的項目對審計目標非常重要,註冊會計師需要單獨對其進行測試,因為零餘額在PPS抽樣中不會被選取。
(4)當發現錯報時,如果風險水平一定,PPS抽樣在評價樣本時可能高估抽樣風險的影響,從而導致註冊會計師更可能拒絕一個可接受的總體賬面金額。
(5)在PPS抽樣中註冊會計師通常需要逐個累計總體金額。但如果相關的會計數據會以電子形式儲存,這不會額外增加大量的審計成本。
(6)當預計總體錯報金額增加時,PPS抽樣所需的樣本規模也會增加。在這些情況下,PPS抽樣的樣本規模可能大予傳統變數抽樣的相應規模。
樣本
PPS抽樣以貨幣單位作為抽樣單元,但註冊會計師卻不是對具體貨幣單位進行審計,而必須確定實物單位(即邏輯單元)來執行審計測試。例如,在表12-14中,註冊會計師要在l~7376(具體金額)之間的總體項目中隨機選取樣本。但是,為了執行審計程式。註冊會計師必須找出l~l2(邏輯單元)之間的總體項目。如果註冊會計師選取的隨機數是3014,則與該數相聯繫的邏輯單元就是6。
PPS樣本可以通過運用計算機軟體、隨機數表或系統抽樣技術來獲取。表12-14列示了一個應收賬款總體,其中包括累計合計數,現以該表來說明如何使用計算機軟體來選取樣本。
表l2一l4應收賬款總體表
| 總體項目(實物單位) | 賬面金額 | 累計合計數(金額單位) |
| 1 | 357 | 357 |
| 2 | 1 281 | 1 638 |
| 3 | 60 | 1 698 |
| 4 | 573 | 2 271 |
| 5 | 69l | 2 962 |
| 6 | 143 | 3 105 |
| 7 | 1 425 | 4 530 |
| 8 | 278 | 4 808 |
| 9 | 942 | 5 750 |
| 10 | 826 | 6 576 |
| 11 | 404 | 6 980 |
| 12 | 396 | 7 376 |
假設註冊會計師想要從表l2-11的總體中,選取一個含有4個賬戶的PPS樣本。由於規定以單位金額為抽樣單位,則總體容量就是7376,因此需要電腦程式隨機生成4個數字。假定電腦程式隨機生成的4個數字是:6586、l756、850、6499,則包含這些隨機金額的總體實物單位項目需由累計合計數欄來確定。它們分別是項目ll(包含6577~6980元的貨幣金額)、項目4(1699~2271元)、項目2(358~l638元)和項目10(5751~6576元)。註冊會計師將對這些實物單位項目進行審計,並將各實物單位頂目的審計結果,套用到它們各自包含的隨機貨幣金額上。
PPS抽樣允許某一實物單位在樣本中出現多次。也就是說,在前例中,如果第四個隨機數改為6880,則樣本項目就是11、4、2和11(6576~6980)。項目11儘管只審計一次,但在統計上仍視為2個樣本項目,樣本中的項目總數也仍然是4個,因為樣本涉及4個貨幣金額數。
PPS抽樣會出現兩個問題,一個問題是:在選樣時,帳面餘額為零的總體項目存在沒有被選取的機會,儘管這些項目可能含有錯報。另外,一些嚴重低估的小餘額被選中的機會也很小。對此,如果註冊會計師關注這些餘額為零或較小的項目,那么解決這一問題的方法是對它們進行一些專門的審計測試。
另一個問題是:PPS抽樣選取的樣本中無法包含負餘額,如應收賬款的貸方餘額等。在進行選樣時,可以先不考慮這些負餘額,而後用其他方法去測試它們。另一種替代方法就是將它們視同正餘額,加入到所要測試的貨幣金額總數中,但這樣做會使分析過程變得複雜化。
推斷
無論選用何種抽樣方法,註冊會計師都必須運用下述方法來推斷總體:根據樣本結果來推斷總體的錯報,確定相應的抽樣誤差。PPS抽樣中根據樣本推斷總體有四方面的重要內容:(1)利用屬性抽樣表來計算結果,但是用可接受的誤受風險代替可接受的信賴過度風險。(2)必須把屬性結果轉換為金額形式。PPS抽樣估計的是總體中錯報的金額,而不是總體中存在錯報的項目百分比。PPS抽樣是通過將每個總體項目定義為單位金額實現這一目的的。因此。估計含有錯報的總體金額比率是估計錯報總額的方法。(3)註冊會計師必須為每個有錯報的總體項目假設一個錯報百分比,這一假設可以使註冊會計師能夠利用屬性抽樣表來估計錯報金額。(4)計算總體錯報界限。錯報界限是在既定可接受的誤受風險下,可能最大的高估額(錯報上限)的估計和可能最大的低估額(錯報下限)的估計。
當樣本中存在錯報和不存在錯報時,註冊會汁師的推斷是不同的。這兩種不同情況下的推斷,將在下面介紹。
(1)未發現錯報時總體的推斷。假設註冊會計師想要對某一應收賬款總體進行函證,以確認其金額的正確性。總體金額為l200000元,並對l00個樣本項目進行了函證。經過審計,在樣本中沒有發現錯報。即使在這種情況下,註冊會計師也要確定總體中可能存在的高估和低估的最大數額。也就是分別確定錯報上限和錯報下限。具體方法如下:假定可接受的誤受風險為5%。使用表12-5,採用與控制測試相同的方法,根據樣本規模(100)和實際的錯報數(0)的交點來確定錯報的上限和下限。表l2-5中該交點處的計算的偏差率上限是3%。既代表錯報上限,也代表錯報下限,均用百分數表示。因為樣本錯報率是0.3%代表抽樣誤差的估計值。
根據樣本結果和從屬性抽樣表中得到的錯報界限,註冊會計師就可以認定,在抽樣風險為5%的條件下,總體錯報金額不會超過3%0為了將這一百分比轉換成貨幣金額,註冊會計師還必須為含有錯報的總體金額假定一個錯報平均百分比。這一假定對錯報界限有著重要影響,為了說明這一影響,我們來考察以下三組假定情況:①高估和低估錯報都是100%;②高估錯報和低估錯報都是10%;③高估錯報為20%,低估錯報為200%。
假定情況①:高估金額等於l00%,低估金額也等於100%,在可接受的誤受風險為5%時錯報界限為:
錯報上限=1200000X3%×l00%=36000(元)
錯報下限=1200000X3%×l00%=36000(元)
被錯報的總體項目錯報額等於其賬面價值總額的這種假定,是對一般情形而言的。由於錯報界限為3%,這些錯報的金額不可能超過36000元(總體賬面金額的3%)。如果所有的錯報都是高估,則高估額就是36。000元。如果所有的錯報都是低估,則低估額也是36000元。
錯報為100%是一個極其保守的假定,特別是對高估來說。假定實際總體偏差率為3%,只有在以下兩種情況同時出現時,36000元才能恰當地反映真實的高估金額。一是所有的錯報額都是高估,因為相抵性錯報額會減少這一高估金額;二是所有錯報總體項目都發生100%的錯報。例如,不會發生將226元的應收餘額誤記為262元的情況,因為這項錯報只有13.7%。(高估262—226=36;36+262=13.7%)。
在計算36000元的高估和低估錯報界限時,註冊會計師並不採用本章前面討論的方法來計算點估計值和抽樣誤差,這是因為從所用表中,可以得出偏差率上限的點估計值和抽樣風險允許限度的數額。儘管沒有計算貨幣單位抽樣的點估計值和抽樣風險允許限度的數額,但它們卻隱含在錯報界限的確定過程之中,並可以根據控制測試的屬性抽樣表來確定。例如;在本例中,點估計值就是零,抽樣風險允許限度就是36000元。
假定情況②:高估金額等於10%,低估金額也等於10%,在可接受的誤受風險為5%時,錯報界限為:
錯報上限=l200000×3%×10%=3600(元)
錯報下限=1200000×3%×10%=3600(元)
一般來說,這種假定是指教錯報項目的錯報額不超過l0%。如果所有項目的錯報都是同一方向,則錯報界限就是3600元。如果將錯報假定由l00%變為l0%,這時對錯報界限會產生重要影響,其影響程度與變動幅度成正比。
假定情況③:高估金額等於20%,低估金額等於200%,在可接受的誤受風險為5%時,錯報界限為:
錯報上限=120000Q×3%×20%=7200(元)
錯報下限=1200000×3%×200%=72000(元r)
低估百分比較大的理由是,,百分比形式的錯誤低估比高估要大得多。例如,一筆應記為200元的應收賬款誤記為20元時,就低估了o00%[(200—20)+20],而一筆應記為20.元的應收賬欹誤記為Z00元時,只高估了90%[(200—20)+200]。
含有較大低估額的項目,由於低估錯報的原因,其賬面價值可能較小,根據貨幣單位抽樣的要義,它們被選人樣本的機會也非常小。有鑒於此,在低估額成為審計關注點時,一些註冊會計師會增加一個由小餘額項目組成的樣本。作為貨幣單位樣本的補充。
為含有錯報的總體項目假定一個恰當的整體錯報百分比,是註冊會計師的一項決策。註冊會計師必須根據具體情況,運用職業判斷來確定這些百分比。在沒有有力的相反證據時,大多數註冊會計師都認為,除非樣本結果中含有錯報;否則將高估額和低估額都假定為l00%是比較合適的。在本章中除非另有說明,錯報假定一律採用100%。
(2)發現錯報時的總體推斷。在上面的討論中,我們假定樣本中沒有錯報。但是如果樣本巾存在錯報又該如何處理呢?這裡仍沿用前面的例子。只是假定樣本中發現了5處錯報,而不是沒有,如表l2—l5所示。
仍用前面討論的根據樣本推斷總體的4項內容,但套用時要做如下修改:
①高估額和低估額分開處理,然後再合併。首先,分別計算出高估額和低估額的初始錯報上限和錯報下限。其次,計算高估和低估的點估計值。初始錯報上限減去低估的點估計值,得出調整後的錯報上限;初始錯報下限減去高估的點估計值,得出調整後的錯報下限。我們將用表l2一l5中的4項高估錯報和一項低估錯報來說明這些計算的方法和原理。
表12-15發現的錯報
| 顧客編號 | 應收賬款帳面金額 | 已審計的應收賬款帳面金額 | 錯報 | 錯報 帳面金額 |
| 2073 | 6 200 | 6 100 | 100 | 0.016 |
| 5lll | 12 910 | 12 000 | 91O | 0.07 |
| 5206 | 4 322 | 4 450 | (128) | (0.03) |
| 7642 | 23 000 | 22 995 | 5 | 0.0002 |
| 9816 | 8 947 | 2 947 | 6 000 | 0.67l |
②對包括零錯報在內的每項錯報,分別做出不同的錯報假定。當樣本中沒有發現錯報時,還需要為總體錯報項目估計一個錯報平均百分比;錯報界限的計算反映了幾種不同的假定。若已經發現了錯報,就可利用樣本信息確定錯報界限。但仍需要錯報假定,只不過此時可以對實際錯報數據加以修改而得。
在發現錯報時,認為所有錯報都是100%的假定不僅異常保守,而且與樣本結果也不一致。在實際工作中常用的假定,也是本書所遵循的假定,就是假定實際的樣本錯報是總體錯報的代表。這一假定要求註冊會計師計算每個樣本項目被錯報的百分比(錯報額/賬面金額),然後把這一百分比套用於總體。表l2一15的最後一欄列示了對每項錯報計算的百分比。對於計算結果中的零錯報部分仍需要做出錯報假定。在本例中對於零錯報部分,高估和低估的錯報界限,都採用了百分之百的錯報假定。
③對控制測試抽樣表中計算的偏差率上限的各層,註冊會計師必須加以處理。這樣做的原因是每項錯報都有不同的錯報假定。在各層的計算時,註冊會計師應首先根據屬性抽樣表來確定每項錯報的計算的偏差率上限,然後再計算出各層。表l2一l6列示了本例根據屬性抽樣表確定的各層∥這裡的層是通過讀取表中樣本規模為100的行,再找到該行與偏差數為0~4列的交點來確定的。
④必須把錯報假定與各個層聯繫起來。其最常用方法就是比較保守地將最大的金額錯報百分比與最大的層相聯繫。表l2一l7就反映了這種聯繫,表中最大的平均錯報是9816號顧客的0.671,而這一錯報是與層係數0.017(也就是發現錯報的最大的層)相聯繫,精確度上限與零錯報層相聯繫部分的假定錯報為100%,這仍然很保守。實際上,表l2一l7反映的是沒有考慮相抵性金額的錯報界限計算j這裡不僅計算錯報上限時假定沒有低估額,而且計算錯報下限時也是假定沒有高估額的。
表l2一l6百分比錯報界限
| 錯報數 | 表中的偏差率上限 | 由各項錯報引起的偏差率上限的增加額(層) |
| 0 | 0.030 | 0.030 |
| 1 | 0.047 | 0.017 |
| 2 | 0.062 | 0.015 |
| 3 | 0.076 | 0.014 |
| 4 | 0.090 | 0.014 |
大多數PPS抽樣法的使用者都認為,在存在相抵性金額時,前面剛討論過的方法過於保守。如果發現了低估金額。則高估金額的界限應當低於未發現低估金額時的界限反之亦然,這是合乎邏輯和常理的。因此,需要為相抵性金額而對界限進行必要的調整,調整的步驟如下:第一步,分別確定高估金額和低估金額的點估計值;第二步,各界限分別減少相對的點估計值。
表12-17計算初始錯報上限和下限的範例
| 錯報數 (1) | 偏差率上限部分 (2) | 賬面價值 (3) | 假定的單位錯報 (4) | 錯報界限部分 (2)x(3)x(4) |
| 高估 O 1 2 3 4 偏差率上限 初始錯報界限 | 0.030 0.017 0.015 0.014 0.014 0.090 | 1 200 000 1 200 000 1 200 0O0 1 200 000 1 200 000 | 1.0 0.67 0.O7 0.016 0.0002 | 36 000 13 688 1 260 269 3 51 220 |
| 低估 0 1 偏差率上限 初始錯報界限 | 0.030 0.017 0.047 | 1 200 000 1 200 000 | 1.0 0.03 | 36 000 612 36 612 |
註:可接受的誤受風險為5%樣本規模為100。
高估的點估計值是已審金額的平均高估額與賬面價值的乘積。低估的點估計值的計算方法與此相同。在本例容趕為l00的樣本中,每一個金額單位有一項金額為3分的低估額。因此,低估的點估計值就是360元(即0.03÷100×1200000)。同理,高估的點估計值就是9086元[(0.671+0.07+0.016+0.0002)÷100×l200000]。
表l2一l8反映了採用這一程式對界限所做的調整。用初始上限51220元與估計最可能的低估額360元相減,得到的差額為50860元,這就是調整後的上限。用初始下限36612元與估計最可能的高估額9086元相減,得到的差額為27526元,這就是調整後的下限。因此,在既定的方法和假定下,註冊會計師就可以得出以下結論:應收賬款高估超過50860元或者低估超過27526元的風險是5%。應當注意,如果錯報假定一旦發生變化,錯報界限也將隨之變化。需要說明的是,這裡採用的依據相抵性金額調整界限的方法,只是目前流行的多種方法中的一種。該方法源於萊斯利、泰托鮑姆和安德森的有關著述。
表l2-18 計算調整錯報界限的示範
| 錯報數 | 單位錯報假定 | 樣本規模 | 帳面總體 | 點估計值 | 界限 |
| 初始高估界限 低估金額 1 調整後的商估界限 | 0.03 | 100 | 1 200 000 | 360 | 51 220 ( 360 ) 50 860 |
| 初始低估界限 高估金額 l 2 3 4 合計 調整後的低估界限 | 0.67l 0.O7 0.016 0.0002 0.7572 | 100 | L 200 000 | 9 086 | 36612 ( 9 086 ) 27 526 |
D·A·菜斯利、泰托鮑姆和R·J·安他森合著:<金額單位抽樣法:註冊會計師的實用指南)。多倫多·庫靜、克拉克和彼特曼出版社1979年版。
以依據表l2—15中的4項高估金額調整錯報上限為例,來演示PPS抽樣中有相抵性金額時,計算調整錯報界限的過程,見表12—18。
同樣,只有錯報下限和錯報上限都完全落在低估和高估可容忍錯報的限額內,註冊會計師才能夠做出總體沒有重大錯報的結論。在本例中,假定註冊會計師已經為應收賬款確定了40000元的可容忍錯報(高債或低估),由於調整後的錯報上限為50860元,超過了40000元的可容忍錯報,因此註冊會計師不能接受總體。