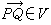簡單介紹
幾何學的一個分支。平面仿射幾何主要研究平面圖形在仿射變換下不改變的性質。平面上的仿射變換仿射幾何學
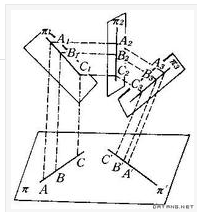
可以看成是連續施行有限回兩個平面之間的平行投影所得到的平面上點之間的一一對應，也可以說仿射變換是一個平行投影“鏈”。如圖，由連續施行平面π到π1，π1到π2，π2到π3，再從π3回到π′的共四次平行投影得到的平面π上點之間的對應，例如A，B，C的對應點為A′，B′，C′，這個對應就是平面π上的一個仿射變換。平面上的仿射變換由三對不共線的對應點完全確定。線段的長度和二直線的交角在仿射變換下一般都要改變。但共線三點A，B，C組成的兩個有向線段AC和BC的量的比AC/BC（稱為A，B，C的簡比）在仿射仿射幾何學
變換下是不改變的，它是仿射變換最基本的不變數。二直線平行這個性質在仿射變換下也不改變。平面上兩個封閉圖形的面積之比，在仿射變換下也是不變的。若一個圖形經過仿射變換變成另一個圖形，就說這兩個圖形是仿射等價的。所有的三角形都與正三角形仿射等價，所有的平行四邊形都與正方形仿射等價，所有的橢圓都與圓仿射等價，所有的雙曲線都與等軸雙曲線仿射等價。在仿射幾何中，互相仿射等價的圖形是不加區別的。
仿射空間
仿射空間中最重要的變換是仿射變換，它的特徵是將共線的三點變為共線的三點。給定仿射坐標系後，仿射變換有明確的代數表示。仿射變換全體構成的變換群稱為仿射變換群。仿射變換下重要的不變性質和不變數有：共線性、平行性、平行線段的長度比等。仿射幾何學
如果在仿射平面（或空間）中引入無窮遠點，並且將它們與原有點不加區別，則就成為射影平面(或空間)。在射影平面（或空間）中指定一條（或一個）直線l(或超平面π)，那么射影變換群中保持l（或π）不動的變換就構成一個與仿射變換群同構的變換子群。從這個意義上講，仿射變換群就是射影變換群的子群，而仿射幾何也就成為射影幾何的子幾何。
過程原由
研究圖形在仿射變換下不變性質的幾何學分支學科。設V是一個 n維向量空間，A是一個集合，其中元素稱為點。如果對A中每兩個點P、Q都惟一對應著V中的一個向量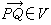
並且這種對應規則還滿足：(1)
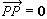(V中零向量),(2)任給P點和V中向量a,總惟一存在點Q使
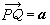，(3)對A中任意三點P、Q、M ，成立
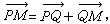則稱A為一個n維仿射空間。n=2時,稱為仿射平面。
在仿射空間中取定一點O，那么任意一點P就惟一地與V中的向量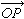
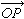對應，稱為P點關於點O的位置向量。點O也常稱為原點。因此，取定原點後，仿射空間A就與向量空間V建立起雙方一一的對應。由此,就可以建立起仿射空間中的仿射坐標系（見坐標系）。
對於向量空間V的k維子空間 Vk(0<k≤n)和A中點P，集合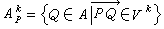
稱為A的仿射子空間，它是過點P的一個k維仿射空間。如果A的子集是仿射空間,必能表為上面形式。特別當k=1時,A
稱為過P的直線;k=2時，稱為平面；k=n-1時，稱為超平面。
仿射空間中最重要的變換是仿射變換，它的特徵是將共線的三點變為共線的三點。給定仿射坐標系後，仿射變換有明確的代數表示。仿射變換全體構成的變換群稱為仿射變換群。仿射變換下重要的不變性質和不變數有：共線性、平行性、平行線段的長度比等。
如果在仿射平面（或空間）中引入無窮遠點，並且將它們與原有點不加區別，則就成為射影平面(或空間)。在射影平面（或空間）中指定一條（或一個）直線l(或超平面π)，那么射影變換群中保持l（或π）不動的變換就構成一個與仿射變換群同構的變換子群。從這個意義上講，仿射變換群就是射影變換群的子群，而仿射幾何也就成為射影幾何的子幾何（見射影幾何學）。
參考書目 蘇步青編：《高等幾何講義》，上海科學技術出版社，上海，1964。
方德植，陳奕培編：《射影幾何》，高等教育出版社，北京，1983。
配圖
仿射幾何學