二項式定理
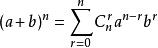 二項展開式
二項展開式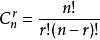 二項展開式
二項展開式 二項展開式
二項展開式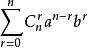 二項展開式
二項展開式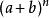 二項展開式
二項展開式其中, ,又有 等記法,稱為二項式係數,此係數亦可表示為楊輝三角形。等式的右邊 即為 的展開式,稱為二項展開式。
理解
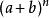 二項展開式
二項展開式 二項展開式
二項展開式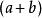 二項展開式
二項展開式 二項展開式
二項展開式 二項展開式
二項展開式 二項展開式
二項展開式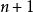 二項展開式
二項展開式 二項展開式
二項展開式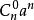 二項展開式
二項展開式 二項展開式
二項展開式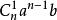 二項展開式
二項展開式 二項展開式
二項展開式 二項展開式
二項展開式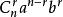 二項展開式
二項展開式 二項展開式
二項展開式 二項展開式
二項展開式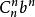 二項展開式
二項展開式將 看成 個 相乘,從每個括弧中取一項 (非 即 ) 相乘的所有單項式合併同類項得到的,按取 的個數分為 類 ,不取 的是 ,取 1 個 的是 ,..., 取 個 的是 ,...,取 個 的是
注意:
(1)選取性,二項式的兩項怎樣選取 (各取幾個) 才能構成所求的項;
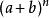 二項展開式
二項展開式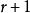 二項展開式
二項展開式 二項展開式
二項展開式 二項展開式
二項展開式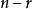 二項展開式
二項展開式 二項展開式
二項展開式 二項展開式
二項展開式 二項展開式
二項展開式(2)有序性, 的展 開式第 項是取 個 (同時取 個 ), 這裡的 和 不能互換
(3)項 、項的係數與二項式係數的區別
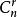 二項展開式
二項展開式某項要把這一項全部寫出來;某項的係數只寫這一項的係數,不帶字母 (即把每個字母當作數 1) ;某項的二項式係數就是相應的組合數
性質
(1)項數:n+1項
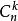 二項展開式
二項展開式(2)第k+1項的二項式係數是
(3)在二項展開式中,與首末兩端等距離的兩項的二項式係數相等。
(4)如果二項式的冪指數是偶數,中間的一項的二項式係數最大。如果二項式的冪指數是奇數,中間兩項的的二項式係數最大,並且相等。
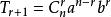 二項展開式
二項展開式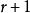 二項展開式
二項展開式(5)二項式通項:,是第項
證明
這裡,採用數學歸納法對二項式定理進行證明
 二項展開式
二項展開式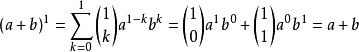 二項展開式
二項展開式當 ,
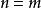 二項展開式
二項展開式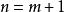 二項展開式
二項展開式假設二項展開式在 時成立,設 ,則:
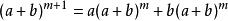 二項展開式
二項展開式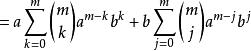 二項展開式
二項展開式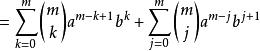 二項展開式
二項展開式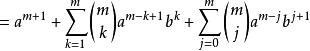 二項展開式
二項展開式 二項展開式
二項展開式(取出 的項)
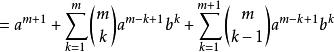 二項展開式
二項展開式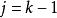 二項展開式
二項展開式(設 )
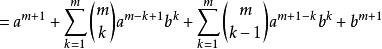 二項展開式
二項展開式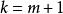 二項展開式
二項展開式( 取出 項)
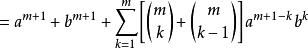 二項展開式
二項展開式(兩者相加)
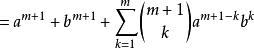 二項展開式
二項展開式(套用帕斯卡法則)
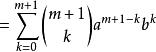 二項展開式
二項展開式等式也成立
結論:對於任意自然數n,等式均成立。
例題
某項的係數
求二項展開式的某項或某項的係數是高考數學的一個基本知識點,每年的高考題都有一定的題出現。
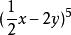 二項展開式
二項展開式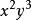 二項展開式
二項展開式例1. 求 的展開式中 的係數
 二項展開式
二項展開式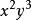 二項展開式
二項展開式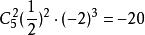 二項展開式
二項展開式解: 要取2個,故 的係數是
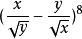 二項展開式
二項展開式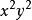 二項展開式
二項展開式例2. 求 的展開式中 的係數
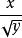 二項展開式
二項展開式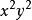 二項展開式
二項展開式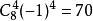 二項展開式
二項展開式解: 要取4個,故的係數是
係數最值項
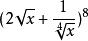 二項展開式
二項展開式例. 求展開式中係數最大項和最小項
解:
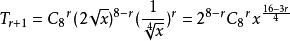 二項展開式
二項展開式通項=
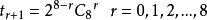 二項展開式
二項展開式通項的係數=
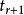 二項展開式
二項展開式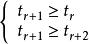 二項展開式
二項展開式設係數 最大,則
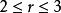 二項展開式
二項展開式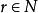 二項展開式
二項展開式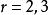 二項展開式
二項展開式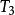 二項展開式
二項展開式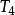 二項展開式
二項展開式解得: ,因為,所以,故係數最大項為和
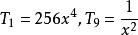 二項展開式
二項展開式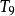 二項展開式
二項展開式由於最大項在中間取得,所以最小項在兩端,計算得:,故係數最小項為
指定項
求二項展開式中的指定項,一般是利用通項公式進行。
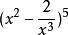 二項展開式
二項展開式例. 展開式中的常數項
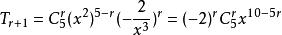 二項展開式
二項展開式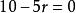 二項展開式
二項展開式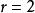 二項展開式
二項展開式解:展開式的通項=,令 ,解得
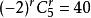 二項展開式
二項展開式故常數項為:

